Problems

Today we’ll look at various problems involving probability. [do we need more of an introduction?]

Today we will focus on applications of the Pythagorean theorem in geometry and number theory. This famous and ancient theorem states that in a right-angled triangle, the area of a square on a hypothenuse (the longest side) is the sum of the areas of the squares on the other two sides. \[a^2 + b^2 = c^2\]

There are over a 100 proofs of Pythagorean theorem, a quite simple one is visible below:

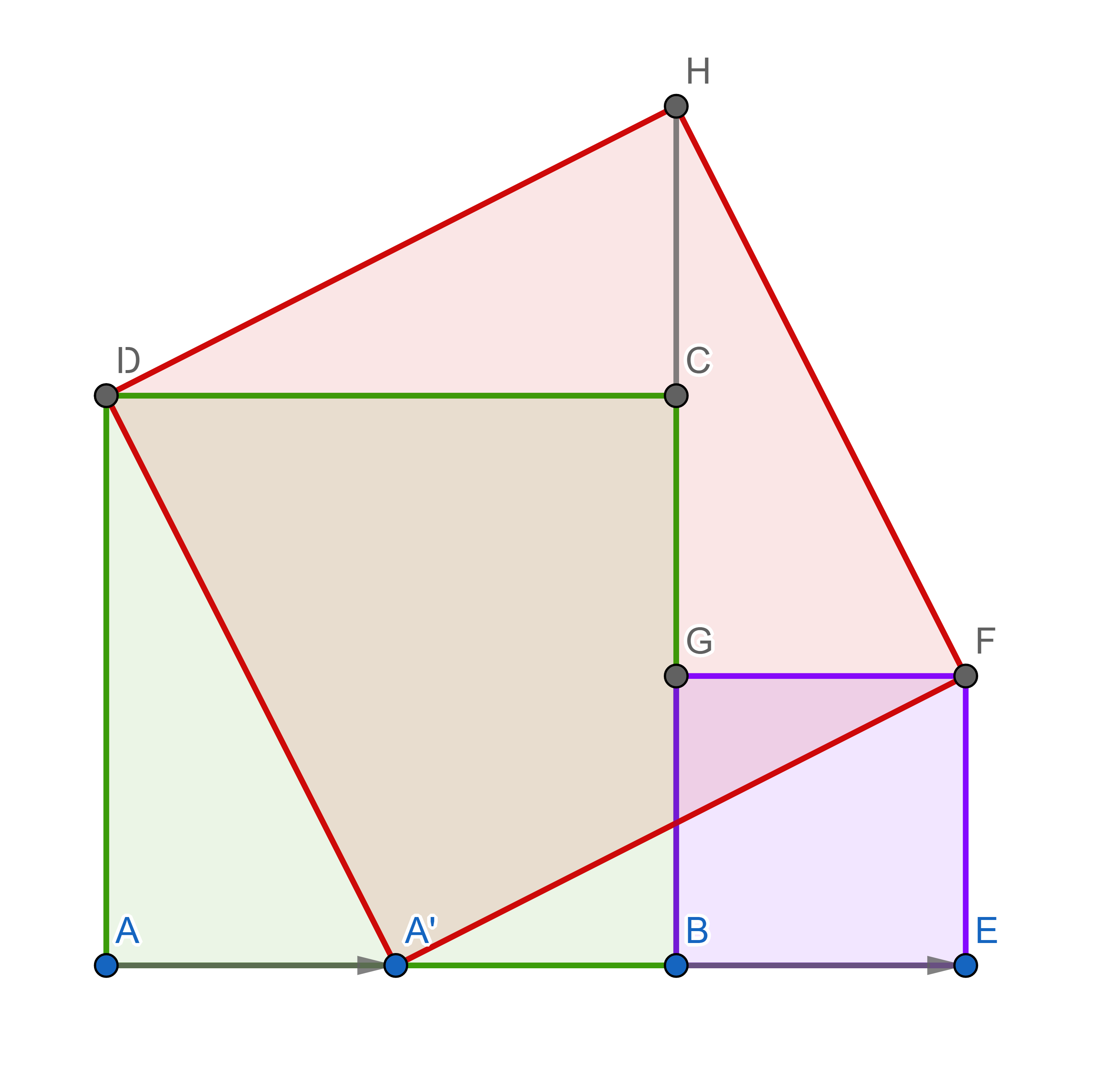
Four right triangles in this picture are identical (congruent): \(\triangle A A' D, \triangle EFA', \triangle GFH\) and \(\triangle CHD\). By moving the triangles around you can see that the large red square has the same area as the sum of areas of the other two squares (violet and green).

Today’s session is not only about geometry, we will also learn something about the equation \(a^2 + b^2 = c^2\), where all the numbers \(a,b,c\) are integers.

You may have seen the first example (seen below) previously. Before we get to that, let’s introduce some notation. We write \(K_n\) for the complete graph on \(n\) vertices - that is, every possible edge is present.

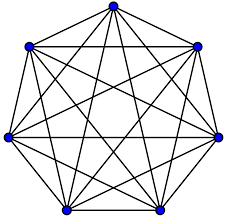
Note that edges don’t have a direction, and are between pairs of different vertices. Ramsey theory looks at what happens when we colour every edge in \(K_n\) either red or blue. Are we guaranteed a red \(K_3\) subgraph? No, because we could just colour every edge in \(K_n\) blue. Instead, we ask if we are guaranteed a red \(K_3\) or a blue \(K_3\) subgraph? It turns out yes, so long as \(n\) is big enough.

We can then look at extensions to this problem. We write \(R(s,t)\) for the least number \(n\) such that whenever you colour the edges of \(K_n\) in red or blue, then you’re guaranteed a red \(K_s\) or a blue \(K_t\). By least \(n\), this means that there’s a colouring of the edges of \(K_{n-1}\) with no red \(K_s\) or blue \(K_t\).

You may like to use the inequality \(R(m,n)\le R(m,n-1)+R(m-1,n)\). Furthermore, when both \(R(m,n-1)\) and \(R(m-1,n)\) are even, we have the stronger inequality of \(R(m,n)\le R(m,n-1)+R(m-1,n)-1\).

It is often the case in geometric situations that figures look very similar, but not quite equal. Two polygons on the plane are called similar if and only if ALL their corresponding angles are equal AND the ratio between ALL the corresponding sides is the same.
The relation between the corresponding sides, in our case it’s \(\frac{|AB|}{|IH|}\), is called the similarity coefficient between the figures. It is common practice to write vertices of similar figures in the order that respects the similarity.

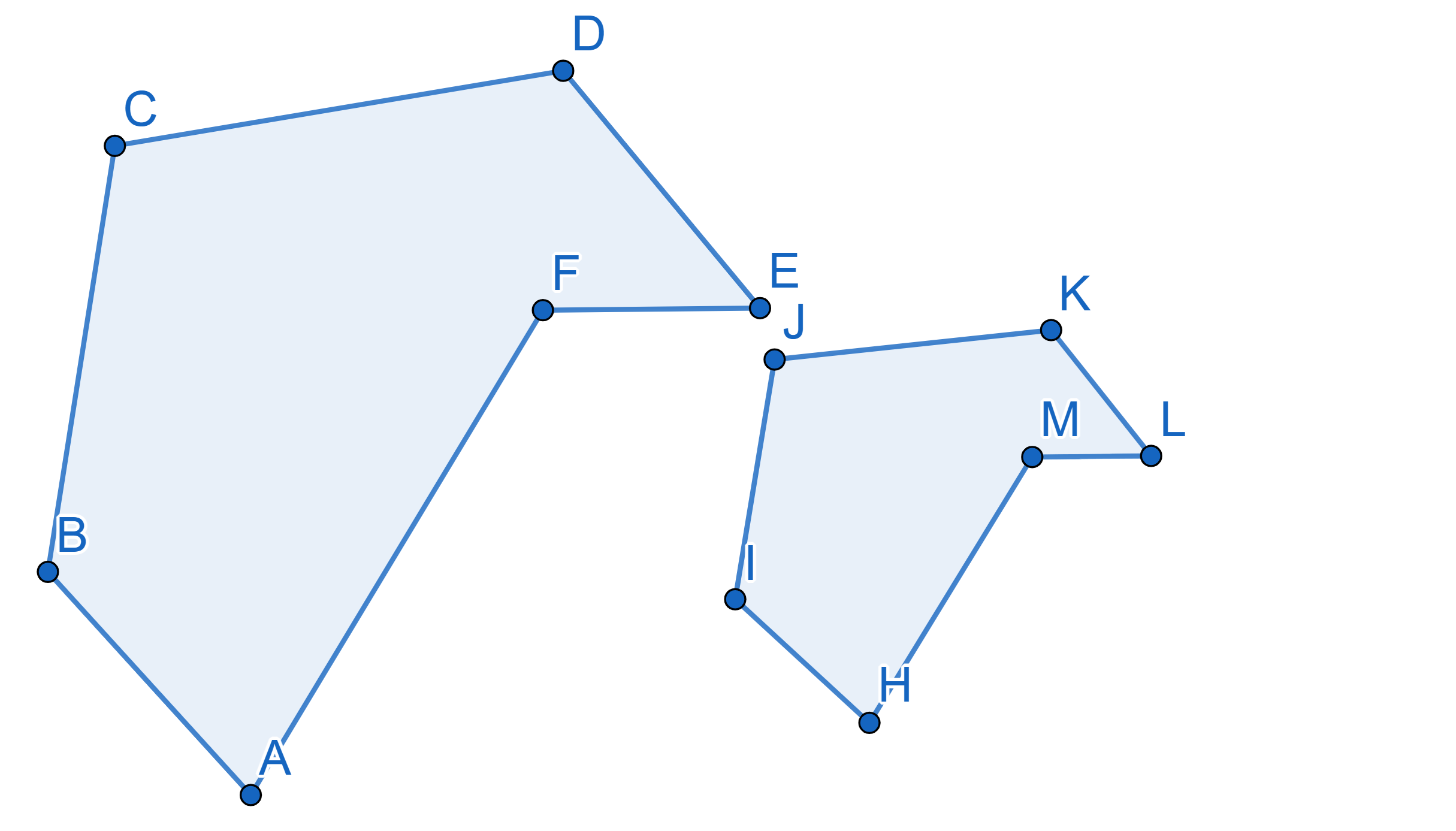
We will find some criteria for determining similarity and apply them to solve problems. The statements of some examples and problems may be helpful for problems coming after them!

Today we’ll look at various logic puzzles where you have to imagine what’s going on inside someone else’s head. What they’re thinking about could be about what’s going on inside your own head!

Today we’ll look at 3-dimensional shapes, including their volumes and surfaces areas. One special kind are the Platonic Solids - the tetrahedron, cube, octahedron, dodecahedron and icosahedron.

Today we will be looking at tilings. We define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated and symmetrical to each other. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that can be extended to cover the entire plane.

We will also look at some tilings of finite shapes, normally rectangles. You can imagine this as tiling a floor. With a huge number of \(1\times2\) tiles, we can investigate how to tile a floor in a rectangular room if no tile can overlap the other. It’s easy to tile the floor in a \(6\times8\) room.

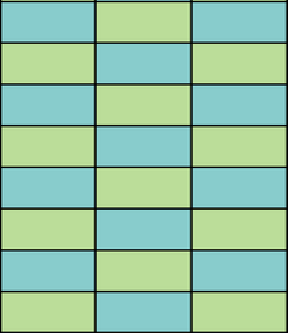
We can notice that if the floor in a room of size \(p\times q\) is tiled with \(1\times2\) tiles, then \(pq\) is even (can you explain why?). The reverse is also true; i.e. if \(pq\) is even, then the floor can be tiled with \(1\times2\) tiles in a similar way to the picture above.

However, this tiling can be cut from one side to another by a grid line without splitting any tiles. Such constructions are impractical, and this type of floor can easily become uneven. That’s why in practise irreducible tilings are used.

A tiling of a rectangle by small identical rectangles (tiles) is called irreducible if any straight cut from one side of the big rectangle to another goes across at least one of the tiles.

We’ll explore how to tile the plane using rectangles, more general quadrilaterals, pentagons and more unconventional shapes. In this exercise sheet, we define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated or reflected to one another. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that we see can be extended to cover the entire plane.

In the majority of today’s problems, one only needs to create a pattern for a small section of the plane, which can then be extended to cover the entire plane through repetition. Such tilings are referred to as periodic. Finding a tiling of the plane using identical shapes that is not periodic, meaning the pattern never repeats itself, has been a long-standing open problem. However, this problem was solved in an article published in March 2023 by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss. The idea of their solution is the following diagram from the article:

The hard part is to prove that this tiling is aperiodic.

In this example we will discuss division with remainder. For polynomials \(f(x)\) and \(g(x)\) with \(\deg(f)\geq \deg(g)\) there always exists polynomials \(q(x)\) and \(r(x)\) such that \[f(x)=q(x)g(x)+r(x)\] and \(\deg(r)<\deg(g)\) or \(r(x)=0\). This should look very much like usual division of numbers, and just like in that case, we call \(f(x)\) the dividend, \(g(x)\) the divisor, \(q(x)\) the quotient, and \(r(x)\) the remainder. If \(r(x)=0\), we say that \(g(x)\) divides \(f(x)\), and we may write \(g(x)\mid f(x)\). Let \(f(x)=x^7-1\) and \(g(x)=x^3+x+1\). Is \(f(x)\) divisible by \(g(x)\)?

In this example we will discuss division with remainder. For polynomials \(f(x)\) and \(g(x)\) with \(\deg(f)\geq \deg(g)\) there always exists polynomials \(q(x)\) and \(r(x)\) such that \[f(x)=q(x)g(x)+r(x)\] and \(\deg(r)<\deg(g)\) or \(r(x)=0\). This should look very much like usual division of numbers, and just like in that case, we call \(f(x)\) the dividend, \(g(x)\) the divisor, \(q(x)\) the quotient, and \(r(x)\) the remainder. If \(r(x)=0\), we say that \(g(x)\) divides \(f(x)\), and we may write \(g(x)\mid f(x)\). Let \(f(x)=x^7-1\) and \(g(x)=x^3+x+1\). Is \(f(x)\) divisible by \(g(x)\)?