We solve problems

Problem #PRU-115447

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

Prove that if the expression

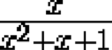
takes a rational value, then the expression

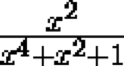
also takes on a rational value.

Problem #PRU-116558

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The nonzero numbers \(a\), \(b\), \(c\) are such that every two of the three equations \(ax^{11} + bx^4 + c = 0\), \(bx^{11} + cx^4 + a = 0\), \(cx^{11} + ax^4 + b = 0\) have a common root. Prove that all three equations have a common root.

Problem #PRU-116704

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The teacher wrote on the board in alphabetical order all possible \(2^n\) words consisting of \(n\) letters A or B. Then he replaced each word with a product of \(n\) factors, correcting each letter A by \(x\), and each letter B by \((1 - x)\), and added several of the first of these polynomials in \(x\). Prove that the resulting polynomial is either a constant or increasing function in \(x\) on the interval \([0, 1]\).

Problem #PRU-116775

Problems Methods Examples and counterexamples. Constructive proofs Pigeonhole principle Pigeonhole principle (other) Set theory and logic Theory of algotithms Theory of algorithms (other)

13–16 4.0

We are given a polynomial \(P(x)\) and numbers \(a_1\), \(a_2\), \(a_3\), \(b_1\), \(b_2\), \(b_3\) such that \(a_1a_2a_3 \ne 0\). It turned out that \(P (a_1x + b_1) + P (a_2x + b_2) = P (a_3x + b_3)\) for any real \(x\). Prove that \(P (x)\) has at least one real root.

Problem #PRU-116817

Problems Methods Algebraic methods Counting in two ways Set theory and logic Mathematical logic Mathematical logic (other)

13–14 3.0

There is a group of 5 people: Alex, Beatrice, Victor, Gregory and Deborah. Each of them has one of the following codenames: V, W, X, Y, Z. We know that:

Alex is 1 year older than V,

Beatrice is 2 years older than W,

Victor is 3 years older than X,

Gregory is 4 years older than Y.

Who is older and by how much: Deborah or Z?

Problem #PRU-32088

Problems Methods Examples and counterexamples. Constructive proofs Pigeonhole principle Pigeonhole principle (other) Set theory and logic Theory of algotithms Theory of algorithms (other)

13–16 4.0

It is known that a certain polynomial at rational points takes rational values. Prove that all its coefficients are rational.

Problem #PRU-32132

Problems Methods Extremal principle Extremal principle (other) Set theory and logic Order relations Algebraic methods Proof by exhaustion

13–15 3.0

The order of books on a shelf is called wrong if no three adjacent books are arranged in order of height (either increasing or decreasing). How many wrong orders is it possible to construct from \(n\) books of different heights, if: a) \(n = 4\); b) \(n = 5\)?

Problem #PRU-32884

Problems Methods Extremal principle Extremal principle (other) Mathematical induction Mathematical induction (other) Algebra and arithmetic Polynomials Polynomial remainder theorem (little Bezout's theorem). Factorisation. Polynomials with integer coefficients and integer values Proof by contradiction Calculus Real numbers Rational and irrational numbers

12–12 3.0

Prove that if the irreducible rational fraction \(p/q\) is a root of the polynomial \(P (x)\) with integer coefficients, then \(P (x) = (qx - p) Q (x)\), where the polynomial \(Q (x)\) also has integer coefficients.

Problem #PRU-35079

Problems Methods Proof by contradiction Calculus Real numbers Rational and irrational numbers

14–15 3.0

Prove that the infinite decimal \(0.1234567891011121314 \dots\) (after the decimal point, all of the natural numbers are written out in order) is an irrational number.

Problem #PRU-35154

Problems Methods Examples and counterexamples. Constructive proofs Pigeonhole principle Pigeonhole principle (other) Set theory and logic Theory of algotithms Theory of algorithms (other)

13–16 4.0

Prove that multiplying the polynomial \((x + 1)^{n-1}\) by any polynomial different from zero, we obtain a polynomial having at least \(n\) nonzero coefficients.