Problems
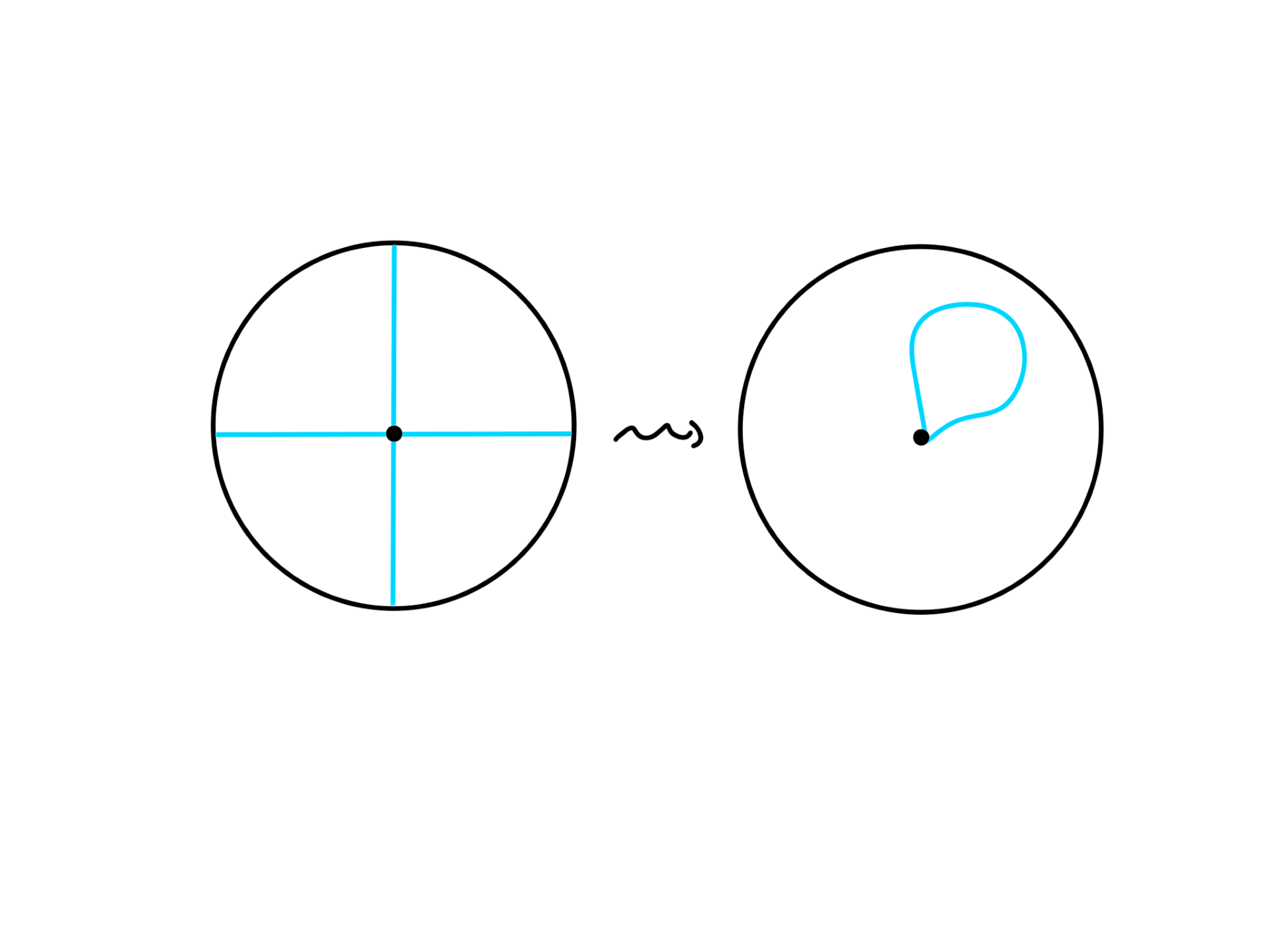
A surface P is created by gluing every pair of antipodal points of a disc (a circle with inside filled in). We represent P on the plane by a disc in the following picture and bear in mind that the antipodal points are glued.
Explain why the two diameters in the pictures are in fact two circles on P and how to stretch it so that it becomes a single loop not touching any of the glued points.
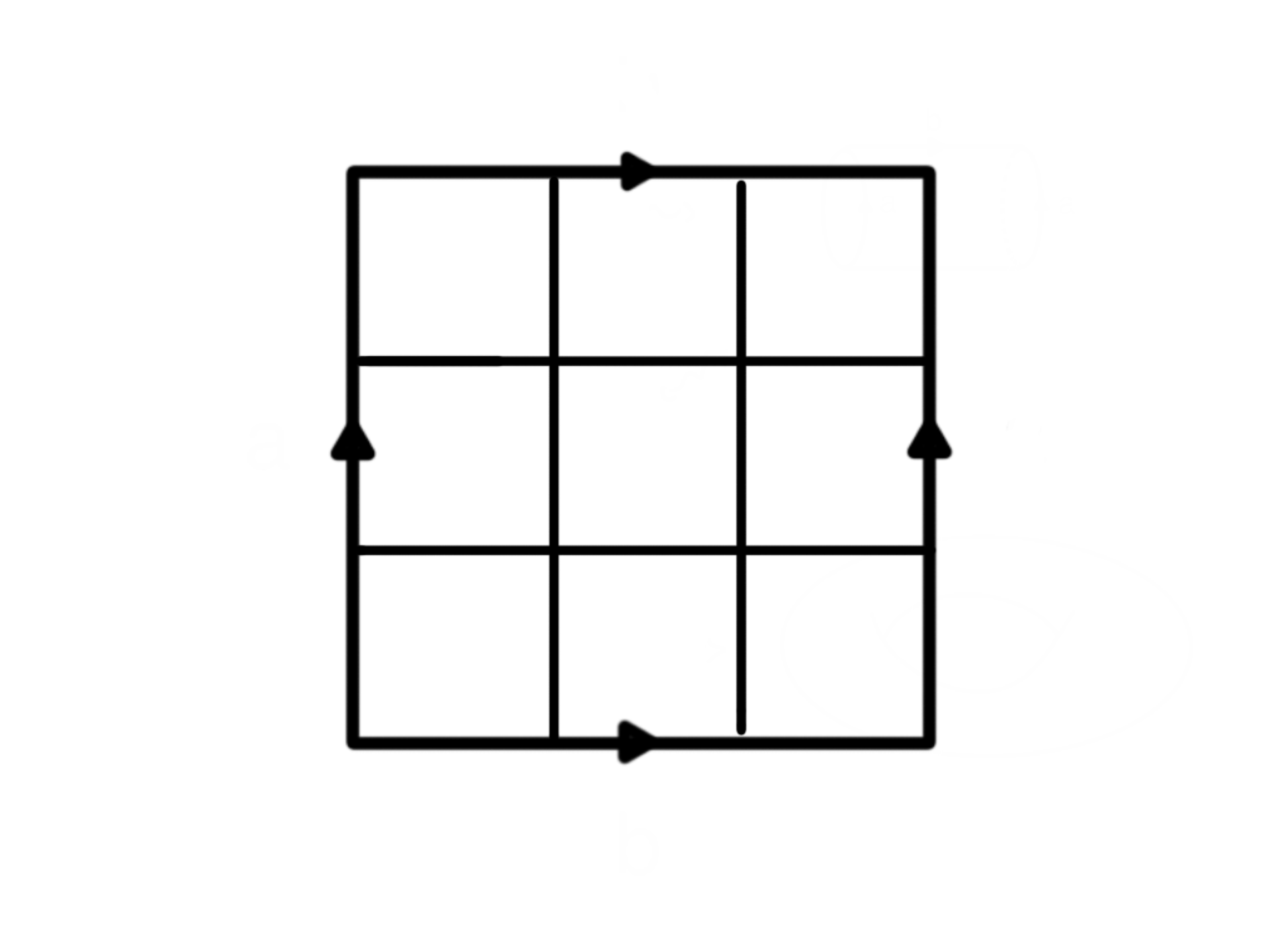
It is possible to play tic-tac-toe on a torus: gluing the sides means that the bottom row is above the top row and the right most column is also to the left of the left most column. Is one of the players guaranteed to win if they play all the right moves?
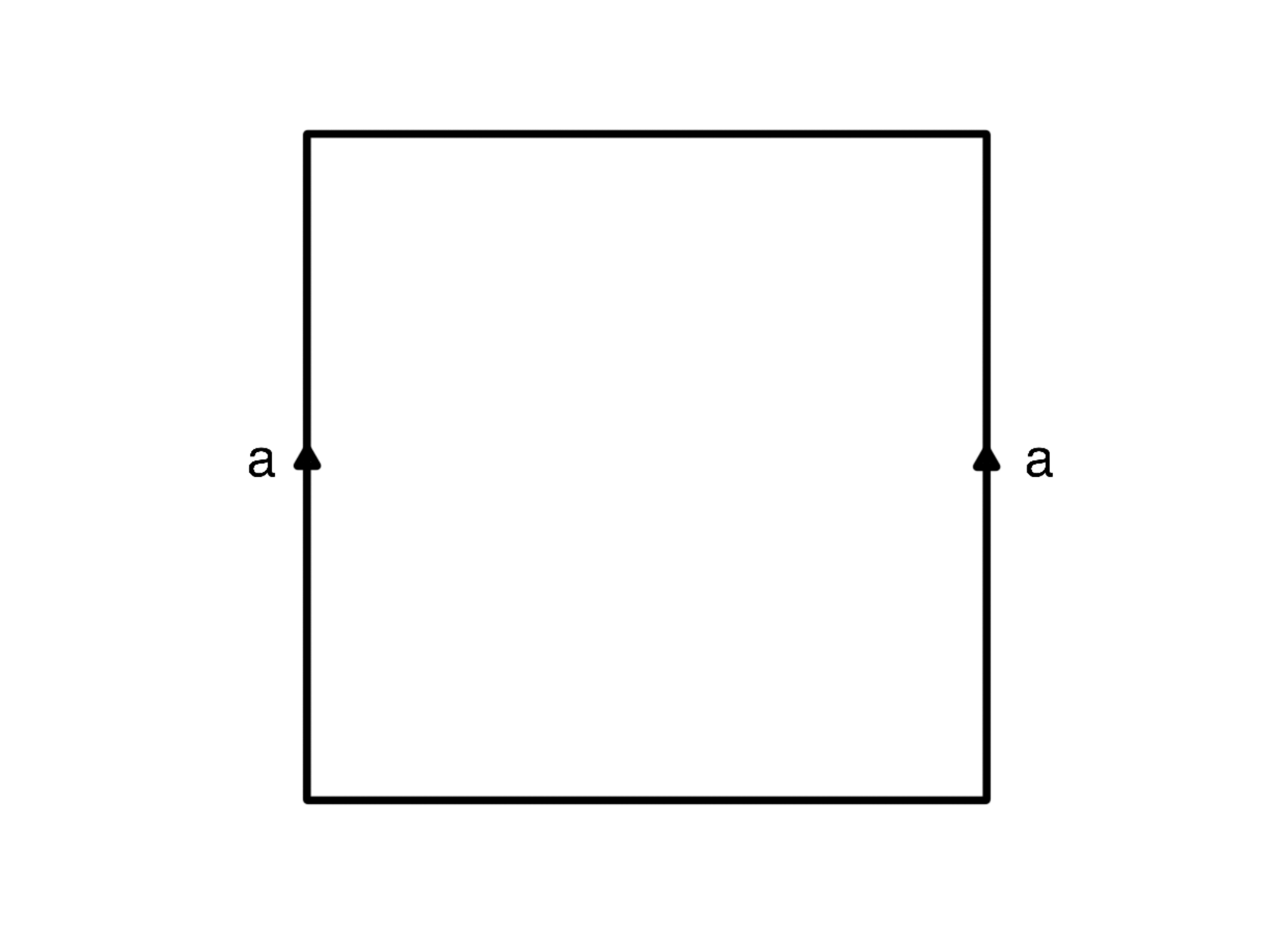
Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the same direction as in the picture.
The picture below shows a closed disc, which is just a circle with the inside filled. The grey interior represents the interior of the disc. Describe the resulting shape when you glue the circular boundary to one point.

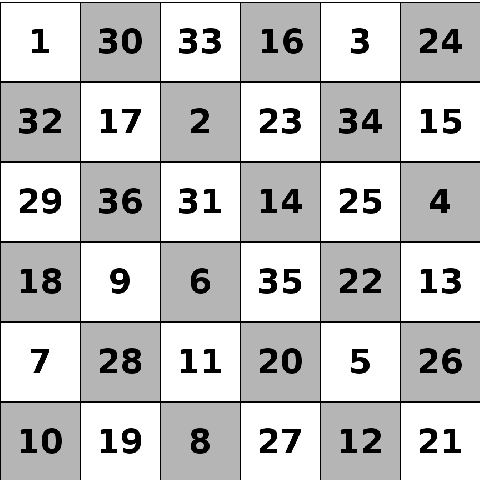
In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.
This is a closed knight’s tour on a \(6\times6\) chessboard.
Can you draw a closed knight’s tour on a \(4\times4\) torus? That is, a \(4\times4\) square with both pairs of opposite sides identified in the same direction, like the diagram below.