Problems

You meet a couple, Dan and Daisy. Dan asks Daisy “Are you the kind who could ask me whether I am a Goop?"
What can be deduced about Dan and Daisy?

You meet an alien (either a Crick or a Goop) called Bobby. He asks you “Am I the kind who could ask whether the wizard is the kind who could ask whether I (Bobby) am the wizard?"
Do you now know for sure who the wizard is?

On the planet of Cricks and Goops, you then meet a strange alien who asks you “Am I the kind who could ask you the question I am now asking?"
What can be said about her?

You meet three friends: Alex, Bernie and Carol. Alex asked Bernie “Are you the kind who could ask Carol whether she is the kind who could ask you whether you two are of different kinds?".
You might realise that it is only possible to deduce the kind of one of the three friends. Which one and are they a Crick or a Goop?

You meet an alien (either a Crick or a Goop) called Charlie. He asks you “Are the wizard and I the same kind?"
Who is the wizard?

On her birthday, my grandma was asked how old she was. She said: "Start with the year I was born. Add the current year to it. Then, from the sum subtract the year I celebrated by \(20\)th birthday. From that, take away the year I was \(30\). The result will be \(16\)." How old is my grandma?

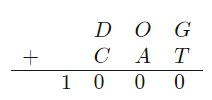
In the long addition above, each letter corresponds to a different digit. What is the sum \(D + O +G + C +A +T\)?

In good conditions, bacteria in a Petri cup spread quite fast, doubling every second. If there was initially one bacterium, then in \(32\) seconds the bacteria will cover the whole surface of the cup.

Now suppose that there are initially \(4\) bacteria. At what time will the bacteria cover the surface of the cup?

A piece containing exactly \(4\) black cells is cut out from a regular \(8\) by \(8\) chessboard. You are only allowed to cut along the edges of the cells and the piece must be connected - namely you cannot have cells attached only with a vertex, they have to share a common edge.

Find the largest possible area of such a piece.

Find all \(n\) such that a closed system of \(n\) gears in a plane can rotate. We call a system closed if the first gear wheel is connected to the second and the \(n\)th, the second is connected to the first and the third, the third is connected to the second and the fourth, the fourth is connected to the third and the fifth, and so on until the \(n\)th is connected to the \(n-1\)th and the first. In the picture, we have a closed system of three gears.