Problems
Can Jennifer draw an octagon and a line passing through two of its vertices in such a way that this line cuts a 10-gon from it?
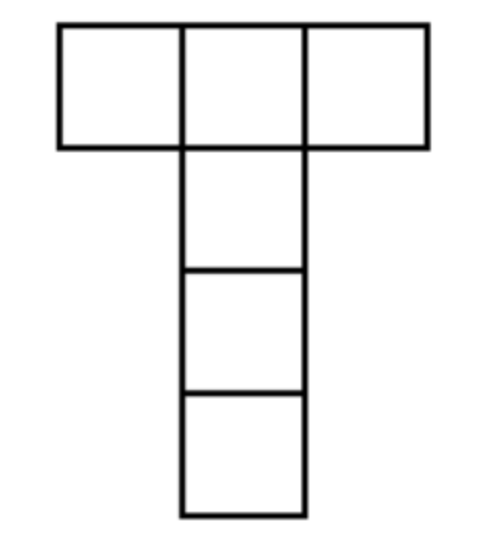
What is the smallest whole number \(n\) such that four identical T-shaped pieces (as shown below) can be placed inside an \(n\times n\) square grid without overlapping?
After having lots of practice with cutting different hexagons with a single cut Jennifer thinks she found a special one. She found a hexagon which cannot be cut into two quadrilaterals. Provide an example of such a hexagon.
Liz is 8 years older than Natasha. Two years ago Liz’s age was 3 times greater than Natasha’s. How old is Liz?
Between them, Jennifer and Alex shared the money they made from running a lemonade stand. Jennifer thought: “If I took \(40\%\) more money then Alex’s share would decrease by \(60\%\)”. How would Alex’s share of the profits change if Jennifer took \(50\%\) more money for herself?
A field that will be used to grow wheat has a rectangular shape. This year, the farmer responsible for this field decided to increase the length of one of the sides by \(20\%\) and decrease the length of another side by \(20\%\). The field remains rectangular. Will the harvest of wheat change this year and, if so, then by how much?
After a circus came back from its country-wide tour, relatives of the animal tamer asked him questions about which animals travelled with the circus.
“Where there tigers?”
“Yes, in fact, there were seven times more tigers than non-tigers.”
“What about monkeys?”
“Yes, there were seven times less monkeys than non-monkeys.”
“Where there any lions?”
What is the answer he gave to this last question?
In a volleyball tournament teams play each other once. A win gives the team 1 point, a loss 0 points. It is known that at one point in the tournament all of the teams had different numbers of points. How many points did the team in second last place have at the end of the tournament, and what was the result of its match against the eventually winning team?
Find the coefficient of \(x\) for the polynomial \((x - a) (x - b) (x - c) \dots (x - z)\).
In a one-on-one tournament 10 chess players participate. What is the least number of rounds after which the single winner could have already been determined? (In each round, the participants are broken up into pairs. Win – 1 point, draw – 0.5 points, defeat – 0).