Problems

A convex polygon on a plane contains no fewer than \(m^2+1\) points with whole number co-ordinates. Prove that within the polygon there are \(m+1\) points with whole number co-ordinates that lie on a single straight line.

A straight corridor of length 100 m is covered with 20 rugs that have a total length of 1 km. The width of each rug is equal to the width of the corridor. What is the longest possible total length of corridor that is not covered by a rug?

The pigeonhole principle is often called “Dirichlet’s box principle". Dirichlet made good use of this tool to show a fundamental result in Diophantine approximation, now commonly known as the Dirichlet Approximation Theorem. You will now prove it yourself!

Suppose \(\alpha\) is any irrational real number and \(N\geq 1\) is any positive integer. Show that there is an integer \(1\leq q\leq N\) and an integer \(p\) such that \[\left| q \alpha - p \right| < \frac{1}{N}.\]

Consider a line segment of length \(3m\). Jack chose \(4\) random points on the segment and measured all the distances between those \(4\) points. Prove that at least one of the distances is less than or equal to \(1m\).

The kingdom of Triangland is an equilateral triangle of side \(10\) km. There are \(5\) cities in this kingdom. Show that some two of them are closer than \(5\) km apart.

Margaret marked three points with integer coordinates on a number line with a red crayon. Meanwhile Angelina marked the midpoint of each pair of red points with a blue crayon. Prove that at least one of the blue points has an integer coordinate.

Margaret and Angelina coloured points in the second dimension. Now Margaret marked five points with both integer coordinates on a plane with a red crayon, while Angelina marked the midpoint for each pair of red points with a blue crayon. Prove that at least one of the blue points has both integer coordinates.

Anna has a garden of square shape with side \(4\) m. After playing with her dog in the garden she left \(5\) dog toys on the lawn. Show that some two of them are closer than \(3\) m apart.

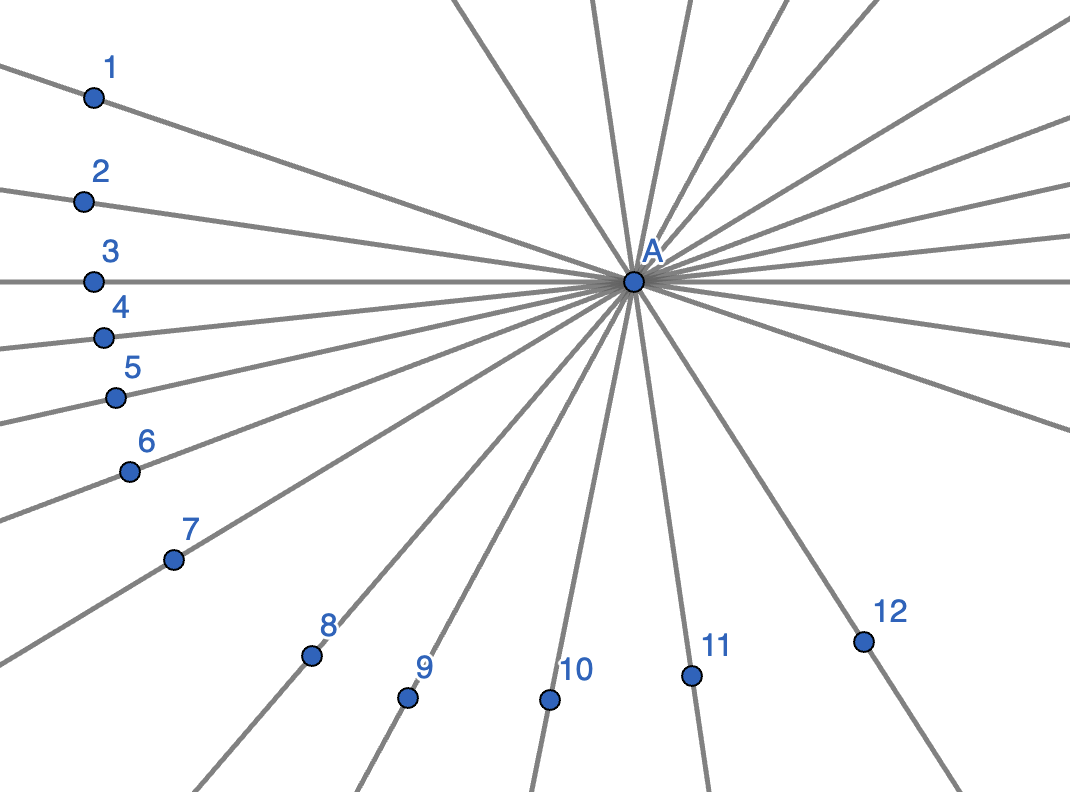
Twelve lines are drawn on the plane, passing through a point \(A\). Prove that there are two of them with angle less than \(17^{\circ}\) between them.

Inside a square of area \(6\), there are three polygons, each of area \(3\). Show that some two of these polygons overlap and the area of the overlap is at least \(1\).