Problems
Why does a mirror reverse right and left instead of up and down?
After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:
how can we cut this into three congruent shapes?
Max asked Emily how old she was. She replied that she was 13 years old the day before yesterday, and will be 16 next year. Then, Max asked her brother, whether it was true, and he said yes. How is it possible if nobody was lying?
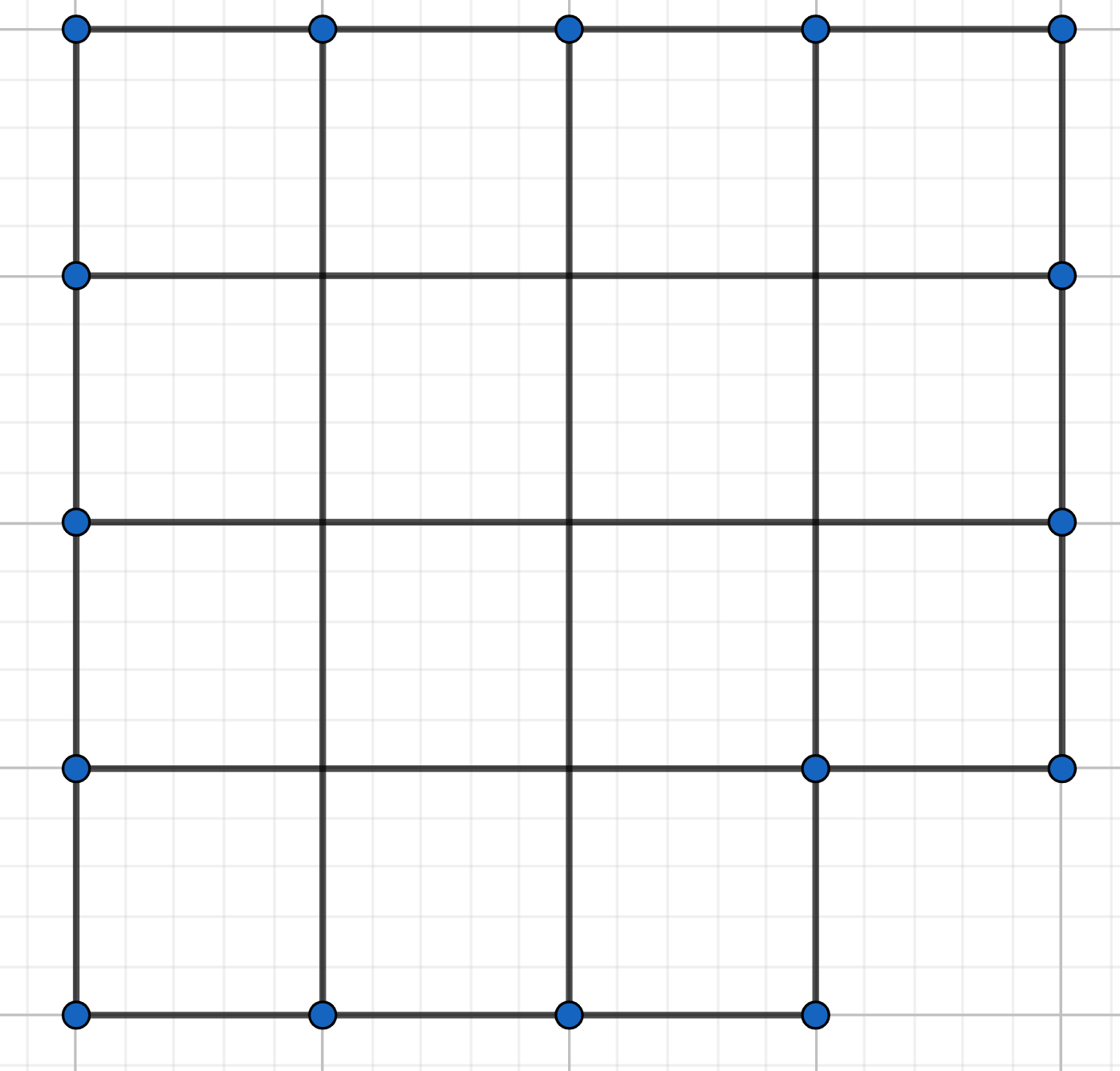
Place coins on a \(6\times 6\) chequered board (one coin on one square), so that all the horizontal lines contain different number of coins, and all vertical lines contain the same number of coins.
A big square was cut into smaller squares. Sebastian used all the pieces and constructed two squares with different side lengths by glueing the pieces together. Show an example of how he could do that.
It was Sebastian’s younger brother who cut the big square in Example 2. Now you need to help him to cut one of the squares (which Sebastian obtained after glueing the pieces) into smaller congruent triangles. But please make sure the elder brother can do the same thing as before: to divide the resulting congruent triangles into two groups and to glue the pieces of each group together to make two squares with different side lengths.
A young and ambitious software engineer is working on his own basic version of an intelligent personal assistant. The application can only answer closed questions (a closed question is a question that can be answered only ‘yes’ or ‘no’). He installs this application on three mobile devices and runs a set of tests. He discovers there is one unstable device. From time to time the application gives wrong answers, but you cannot really predict when. Being exhausted after unsuccessful attempts to find the mistake in his code, the software engineer goes to sleep. The next morning he cannot remember which device is not working properly. Taking into account that devices are connected to the same server (so normally working applications can detect which one is not always receiving the signal) explain how in two questions the engineer can determine the unstable device. One question is for one device only.
Assume you have a chance to play the following game. You need to put numbers in all cells of a \(10\times10\) table so that the sum of numbers in each column is positive and the sum of numbers in each row is negative. Once you put your numbers you cannot change them. You need to pay £1 if you want to play the game and the prize for completing the task is £100. Is it possible to win?
A pencil box contains pencils of different colours and different lengths. Show that it is possible to choose two pencils of both different colours and different lengths.
Once again consider the game from Example 2.
(a) Will you change your answer if the field is a rectangle?
(b) The rules are changed. Now you win if the sum of numbers in each row is greater than 100 and the sum of the numbers in each column is less than 100. Is it possible to win?