Problems
Is it possible to cover a \(10 \times 10\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
On a \(9\times 9\) board \(65\) bugs are placed in the centers of some of the squares. The bugs start moving at the same time and speed to a square that shares a side with the one they were in. When they reach the center of that square, they make a \(90\) degrees turn and keep walking (without leaving the board). Prove that at some moment of time there are two bugs in the same square. Note: When they turn it can be either to the right or to the left.
A \((2n - 1) \times (2n - 1)\) board is tiled with pieces of the following possible types:
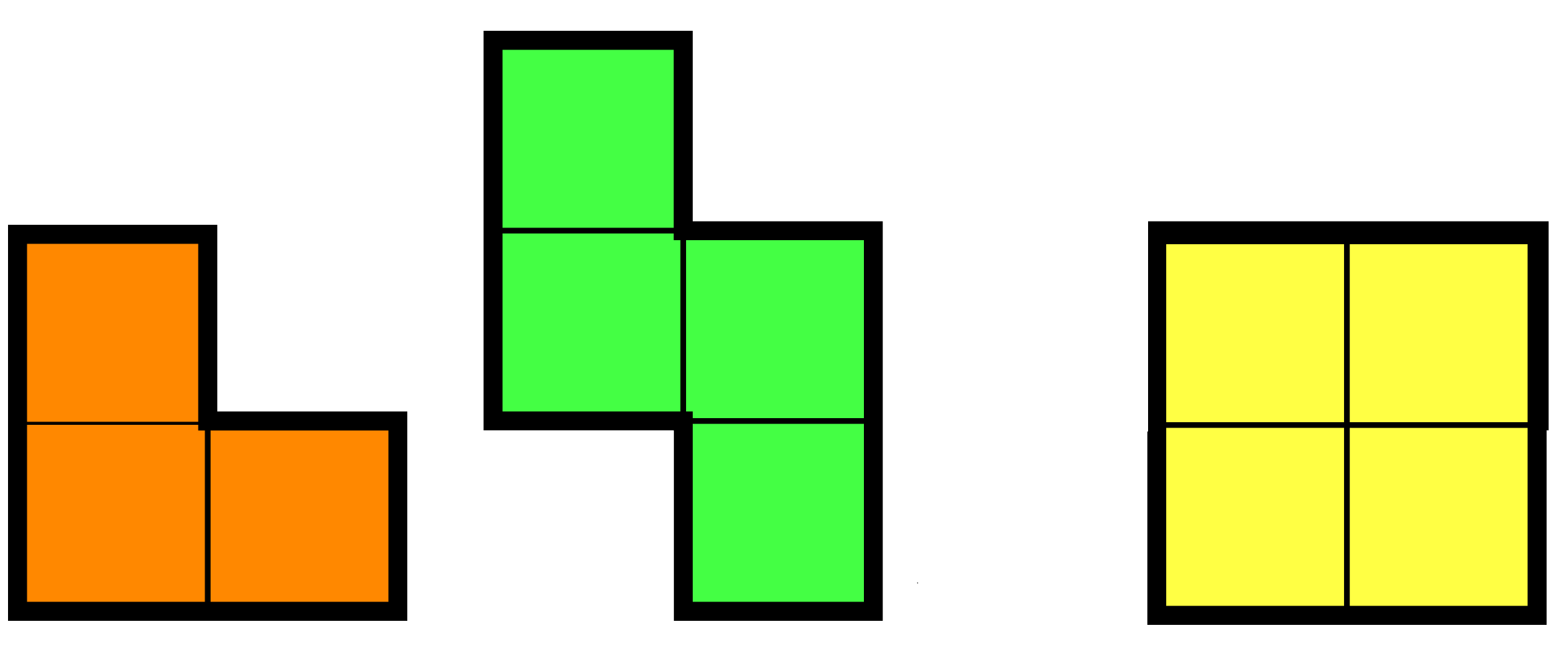
Prove that at least \(4n-1\) of the first type have been used.
In an \(n \times n\) board the squares are painted black or white in some way. Three of the squares in the corners are white and one is black. Show that there is a \(2\times 2\) square with an odd number of white unit squares.
On an \(8\times 8\) board there is a lamp in every square. Initially every lamp is turned off. In a move we choose a lamp and a direction (it can be the vertical direction or the horizontal one) and change the state of that lamp and all its neighbours in that direction. After a certain number of moves, there is exactly one lamp turned on. Find all the possible positions of that lamp.
In an \(5\times 5\) board one corner was removed. Is it possible to cover the remaining board with linear trominos (\(1\times 3\) blocks)?
Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
How many five-digit numbers are there which are written in the same from left to right and from right to left? For example the numbers \(54345\) and \(12321\) satisfy the condition, but the numbers \(23423\) and \(56789\) do not.