Problems

We’re told that Leonhard and Carl are knights or liars (the two of them could be the same or one of each). They have the following conversation.

Leonhard says “If \(49\) is a prime number, then I am a knight."

Carl says “Leonhard is a liar".
Prove that Carl is a liar.

A family is going on a big holiday, visiting Austria, Bulgaria, Cyprus, Denmark and Estonia. They want to go to Estonia before Bulgaria. How many ways can they visit the five countries, subject to this constraint?

How many subsets of \(\{1,2,...,n\}\) (that is, the integers from \(1\) to \(n\)) have an even product? For the purposes of this question, take the product of the numbers in the empty set to be \(1\).

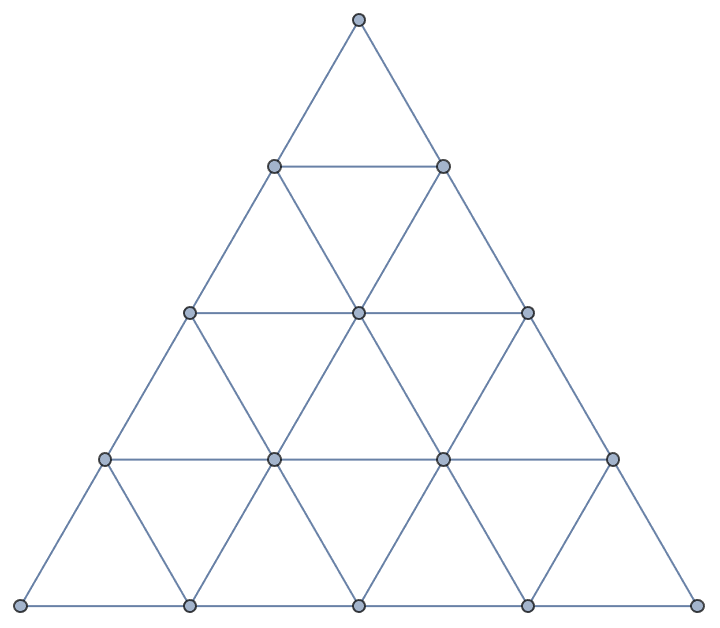
In the following grid, how many different ways are there of getting from the bottom left triangle to the bottom right triangle? You must only go from between triangles that share an edge and you can visit each triangle at most once. (You don’t have to visit all of the triangles.)

You and I are going to play a game. We have one million grains of sand in a bag. We take it in turns to remove \(2\), \(3\) or \(5\) grains of sand from the bag. The first person that cannot make a move loses.

Would you go first?

There are \(n\) balls labelled 1 to \(n\). If there are \(m\) boxes labelled 1 to \(m\) containing the \(n\) balls, a legal position is one in which the box containing the ball \(i\) has number at most the number on the box containing the ball \(i+1\), for every \(i\).

There are two types of legal moves: 1. Add a new empty box labelled \(m+1\) and pick a box from box 1 to \(m+1\), say the box \(j\). Move the balls in each box with (box) number at least \(j\) up by one box. 2. Pick a box \(j\), shift the balls in the boxes with (box) number strictly greater than \(j\) down by one box. Then remove the now empty box \(m\).

Prove it is possible to go from an initial position with \(n\) boxes with the ball \(i\) in the box \(i\) to any legal position with \(m\) boxes within \(n+m\) legal moves.

Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.

Today you saw two infinitely long buses with seats numbered as \(1,2,3,...\) carrying infinitely many guests each arriving at the full hotel. How do you accommodate everyone?

Now there are finitely many infinitely long buses with seats numbered as \(1,2,3,...\) carrying infinitely many guests each arriving at the full hotel. Now what do you do?

How about infinitely many very long buses with seats numbered \(1,2,3...\), each carrying infinitely many guests, all arriving at the hotel. Assume for now that the hotel is empty. But that seems like a lot of guests to accommodate. What should you do?