Problems

How many subsets of \(\{1, 2, . . . , n\}\) are there of even size?

In how many ways can \(\{1, . . . , n\}\) be written as the union of two sets? Here, for example, \(\{1, 2, 3, 4\}\cup\{4, 5\}\) and \(\{4, 5\}\cup\{1, 2, 3, 4\}\) count as the same way of writing \(\{1, 2, 3, 4, 5\}\) as a union.

Prove for any natural number \(n\) that \((n + 1)(n + 2). . .(2n)\) is divisible by \(2^n\).

Consider a set of natural numbers \(A\), consisting of all numbers divisible by \(6\), let \(B\) be the set of all natural numbers divisible by \(8\), and \(C\) be the set of all natural numbers divisible by \(12\). Describe the sets \(A\cup B\), \(A\cup B\cup C\), \(A\cap B\cap C\), \(A-(B\cap C)\).

Prove that the set of all finite subsets of natural numbers \(\mathbb{N}\) is countable. Then prove that the set of all subsets of natural numbers is not countable.

In a distant village, there are \(3\) houses and \(3\) wells. Inhabitants of each house want to have access to all \(3\) wells. Is it possible to build non-intersecting straight paths from each house to each well? All houses and well must be level (that is, none of them are higher up, like on a mountain, nor are any of them on lower ground, like in a valley).

A parliament has 650 members. In this parliament there is only one house and every member has at most three enemies. We wish to split this parliament into two separate houses in such a way that each member will have at most one enemy in the same house as them. We assume that hard feelings among members of parliament are mutual, namely if \(A\) recognises \(B\) as their enemy, then \(B\) also recognises \(A\) as their enemy.

Is this splitting possible?

How many subsets are there of \(\{1,2,...,n\}\) (the integers from \(1\) to \(n\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

A round-robin tournament is one where each team plays every other team exactly once. Five teams take part in such a tournament getting: \(3\) points for a win, \(1\) point for a draw and \(0\) points for a loss. At the end of the tournament the teams are ranked from first to last according to the number of points.
Is it possible that at the end of the tournament, each team has a different number of points, and each team except for the team ranked last has exactly two more points than the next-ranked team?

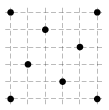
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.