Problems

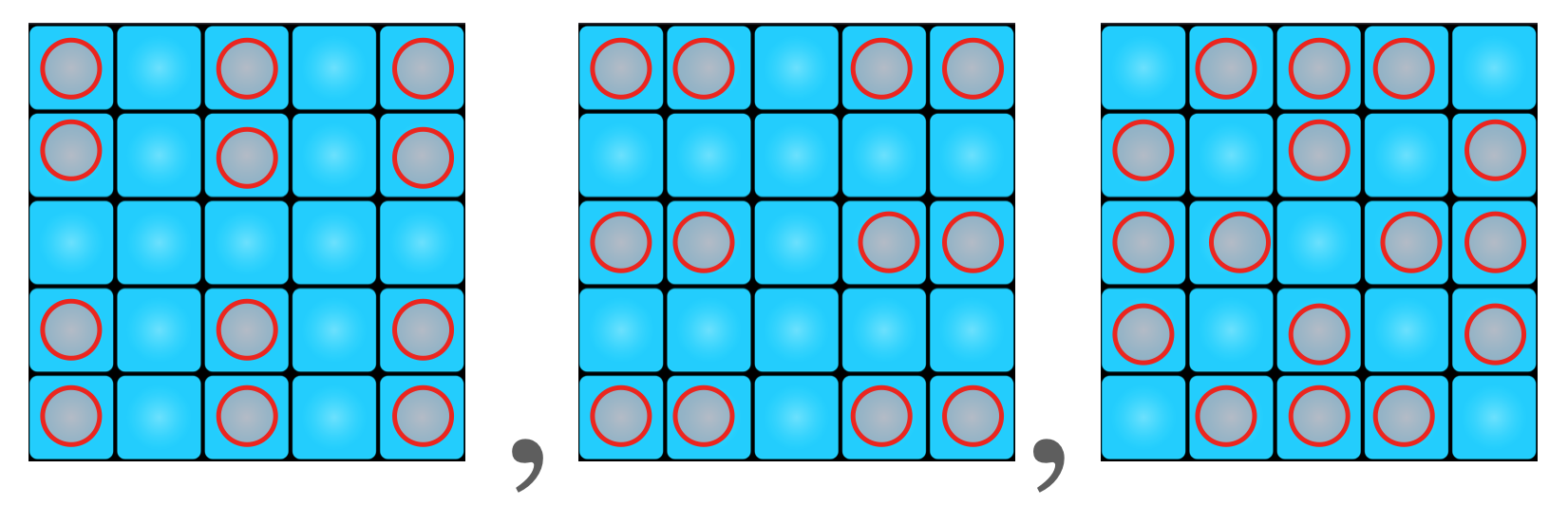
George is playing on the \(5\times 5\) “Lights Out" board and says that since each light can be on or off, and there are \(25\) lights on the board, the number possible light patterns that can be achieved by playing the game is \(2^{25}\). It turns out that the number is much smaller, it is \(2^{23}\). Can you explain why? You may take it as a fact that these three are the only quiet plans of the \(5\times 5\) board:

Alice was playing on the \(5\times 5\) lights out board and obtained this light pattern:

how did she obtain it?

After some playing with the \(3\times 3\) board, Sam guessed that there were \(900\) different light patterns that could be obtained by playing on this board. Was he right?

The original “Lights Out” game works like this: a light pattern is shown on the board, and your task is to turn all the lights off. A light pattern is called solvable if you can complete the game starting from that pattern. Ziheng and Jan are playing on an \(n\times n\) board, and they notice that some patterns are unsolvable. Can you find a rule to decide when a pattern is not solvable?