Problems
Prove that it’s impossible to cover a \(4\times9\) rectangle with \(9\) ‘T’ tetrominoes (one copy seen in red).


Adi and Maxim play a game. There are \(100\) sweets in a bowl, and they each take in turns to take either \(2\), \(3\) or \(4\) sweets. Whoever cannot take any more sweets (since the bowl is empty, or there’s only \(1\) left) loses.
Maxim goes first - who has the winning strategy?
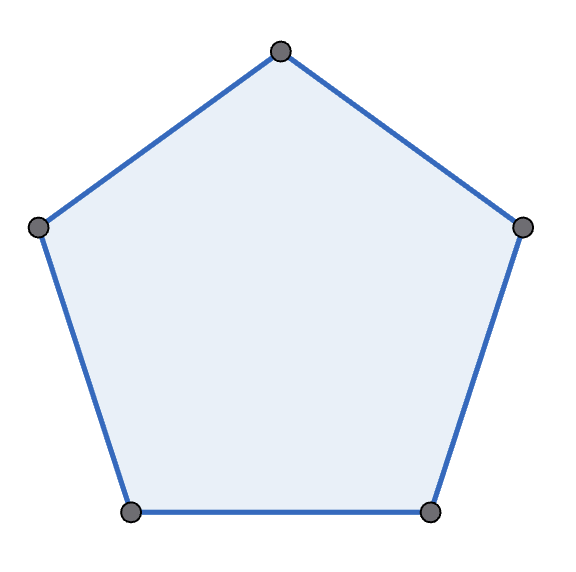
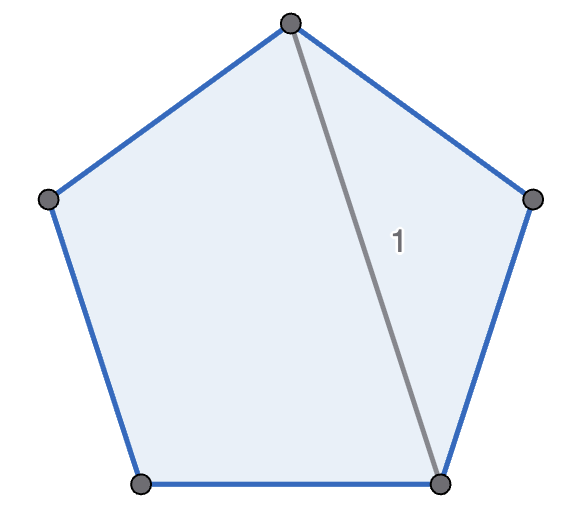
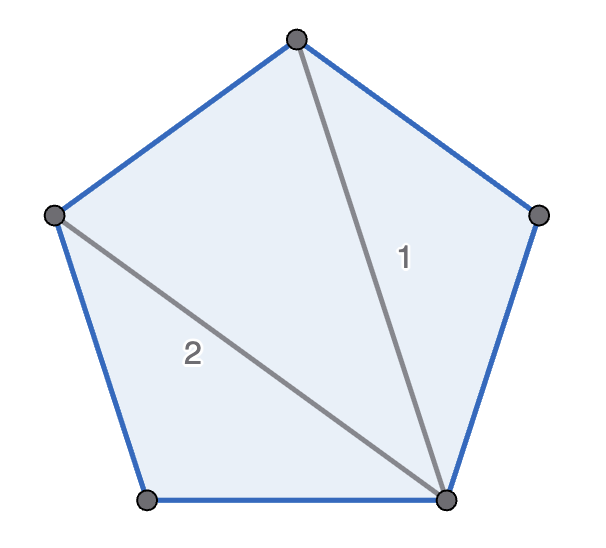
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).
One square is coloured red at random on an \(8\times8\) grid. Show that no matter where this red square is, you can cover the remaining \(63\) squares with \(21\) ‘L’ triominoes, with no gaps or overlaps.

Explain why you can’t rotate the sides on a normal Rubik’s cube to get to the following picture (with no removing stickers, painting, or other cheating allowed).

How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?
The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?
There are two hourglasses, a small one and a large one. The sand in the small one takes \(7\) minutes to fall all the way through, and the sand in the large one takes \(11\) minutes. How can you measure \(15\) minutes using those?
Imagine a \(2\times 2\) “Lights Out" board. If every light is off at the start, how can we turn on just one of the squares? Can you notice something about the order in which we press squares?
Suppose we have a \(2\times 2\) board where all the lights start being turned off, how can we turn on the top two lights?