Problems

To transmit messages by telegraph, each letter of the Russian alphabet () ( and are counted as identical) is represented as a five-digit combination of zeros and ones corresponding to the binary number of the given letter in the alphabet (letter numbering starts from zero). For example, the letter is represented in the form 00000, letter -00001, letter -10111, letter -11111. Transmission of the five-digit combination is made via a cable containing five wires. Each bit is transmitted on a separate wire. When you receive a message, Cryptos has confused the wires, so instead of the transmitted word, a set of letters is received. Find the word you sent.

In one urn there are two white balls, in another two black ones, in the third – one white and one black. On each urn there was a sign indicating its contents: WW, BB, WB. Someone rehung the signs so that now each sign indicating the contents of the urn is incorrect. It is possible to remove a ball from any urn without looking into it. What is the minimum number of removals required to determine the composition of all three urns?

a) There are 21 coins on a table with the tails side facing upwards. In one operation, you are allowed to turn over any 20 coins. Is it possible to achieve the arrangement were all coins are facing with the heads side upwards in a few operations?

b) The same question, if there are 20 coins, but you are allowed to turn over 19.

You may remember the game Nim. We will now play a slightly modified version, called Thrim. In Thrim, there are two piles of stones (or any objects of your choosing), one of size \(1\) and the other of size \(5\).
Whoever takes the last stone wins. The players take it in turns to remove stones - they can only remove stones from one pile at a time, and they can remove at most \(3\) stones at a time.
Does the player going first or the player going second have a winning strategy?

Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.

Explain why a position \(g\) is a winning position if there is a move that turns \(g\) into a losing position. On the other hand, explain why a position is a losing position if all moves turns it into a winning position.

A technique that can be used to completely solve certain games is drawing game graphs. Given a game \(G\), we draw an arrow pointing from a position \(g\) to a position \(h\) if there is a move from \(g\) to \(h\).

As a simple example, the game graph of \(\text{Nim}(2)\) is shown below.

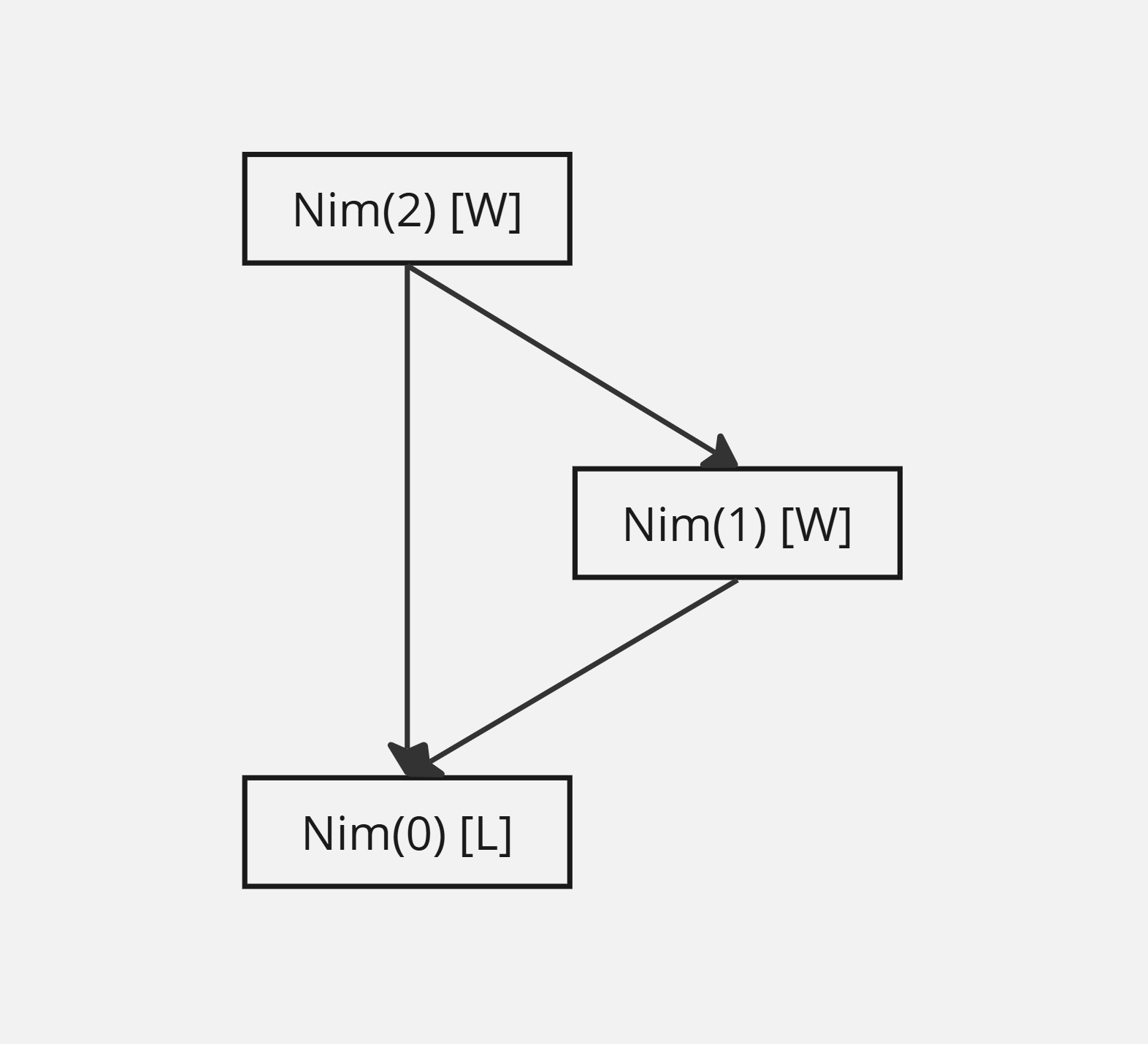
Draw the game graph of \(\text{Nim}(2,2)\). Is \(\text{Nim}(2,2)\) a winning position or losing position?

Is \(\text{Nim}(2,5)\) a winning position or a losing position?

Let \(x,y\) be nonnegative integers. Determine when \(\text{Nim}(x,y)\) is a losing position and when it is a winning position.

Is \(\text{Nim}(1,2,3)\) a winning position or a losing position?