Problems

Is it possible to tile a \(3\times20\) rectangle with the twelve pentominoes?

How can we tile the plane with this cube net?

How can we tile the plane with this cube net?

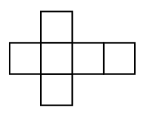
Imagine a \(5\times6\) rectangular chocolate bar, and you want to split it between you and your \(29\) closest friends, so that each person gets one square. You repeatedly snap the chocolate bar along the grid lines until the rectangle is in \(30\) individual squares. You can’t snap more than one rectangle at a time.

The diagram shows a couple of choices for your first two snaps. For example, in the first picture, you snap along a vertical line, and then snap the left rectangle along a horizontal line.
How many snaps do you need to get the \(30\) squares?

Prove that it’s impossible to cover a \(4\times9\) rectangle with \(9\) ‘T’ tetrominoes (one copy seen in red).

One square is coloured red at random on an \(8\times8\) grid. Show that no matter where this red square is, you can cover the remaining \(63\) squares with \(21\) ‘L’ triominoes, with no gaps or overlaps.

How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?

The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?