Problems
There are two stacks of coins on a table: in one of them there are 30 coins, and in the other – 20. You can take any number of coins from one stack per move. The player who cannot make a move is the one that loses. Which player wins with the correct strategy?
The rook stands on the square a1 of a chessboard. For a move, you can move it by any number of cells to the right or up. The one who puts the rook on the h8 square will win. Who wins with the right strategy?
Explain why a position \(g\) is a winning position if there is a move that turns \(g\) into a losing position. On the other hand, explain why a position is a losing position if all moves turns it into a winning position.
A technique that can be used to completely solve certain games is drawing game graphs. Given a game \(G\), we draw an arrow pointing from a position \(g\) to a position \(h\) if there is a move from \(g\) to \(h\).
As a simple example, the game graph of \(\text{Nim}(2)\) is shown below.
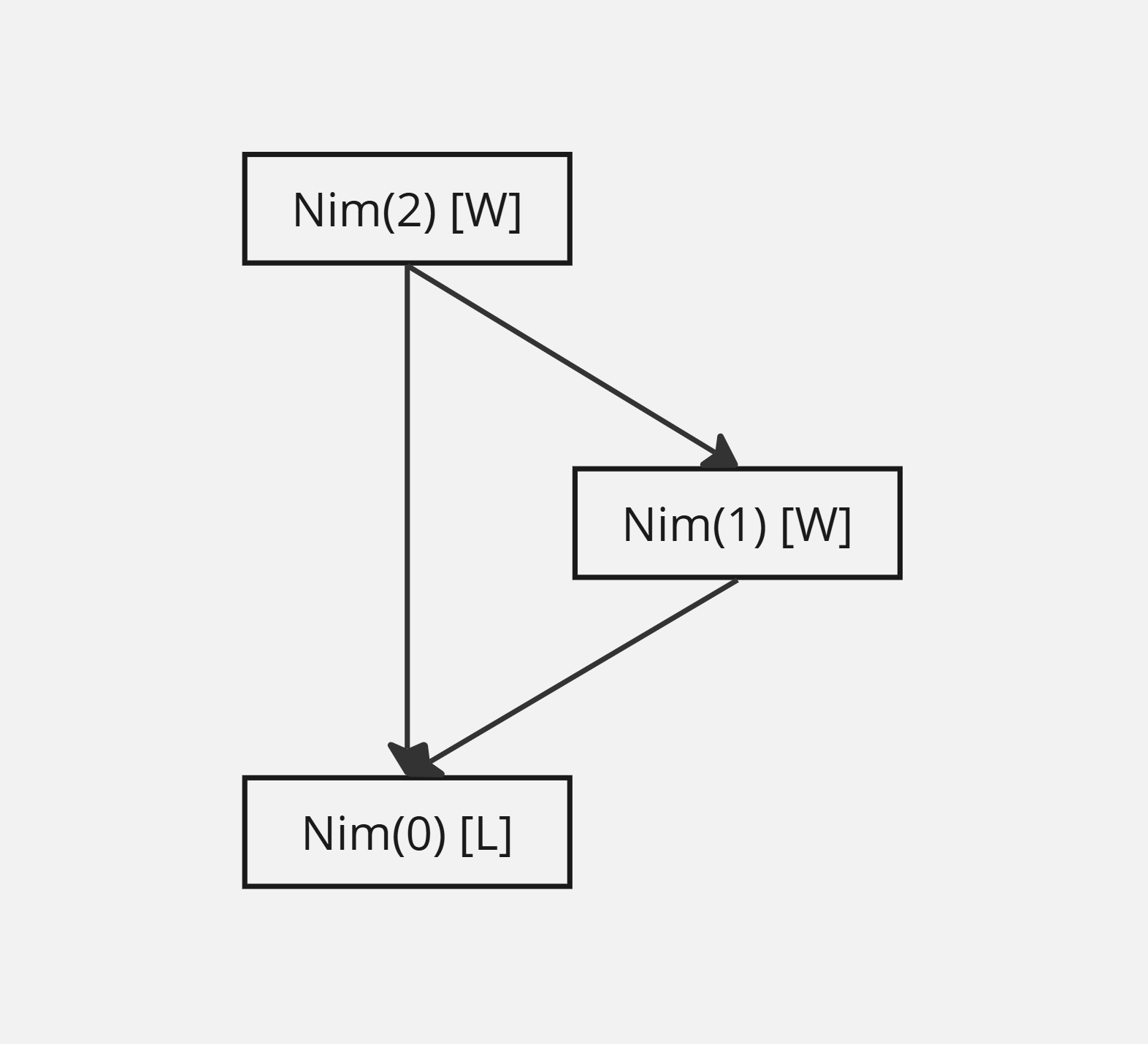
Draw the game graph of \(\text{Nim}(2,2)\). Is \(\text{Nim}(2,2)\) a winning position or losing position?
Is \(\text{Nim}(2,5)\) a winning position or a losing position?
Let \(x,y\) be nonnegative integers. Determine when \(\text{Nim}(x,y)\) is a losing position and when it is a winning position.
Is \(\text{Nim}(1,2,3)\) a winning position or a losing position?
Is \(\text{Nim}(1,2,4,5,5)\) a winning position or a losing position?
Let us define XOR (or addition mod 2). XOR is defined for 0 and 1 only. Here is a table recording the values of XOR:
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Now we define the important concept of nim-sum. Given two natural numbers \(x\) and \(y\), we first convert them into binary representations and then compute XOR on individual digits. The resulting number, denoted \(x \oplus y\), is the nim-sum of \(x\) and \(y\). Here is an example.
| 1 | 0 | 1 | 1 | 0 | |
| XOR | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
This is simply saying \(22 \oplus 5 = 19\). Note that \(22=(10110)_2\) and \(5=(00101)_2\).
Verify \((x \oplus y) \oplus z = x \oplus (y \oplus z)\), so we can speak of \(x \oplus y \oplus z\) with no ambiguity.
Show that \(x \oplus y = 0\) if and only if \(x = y\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).