Problems

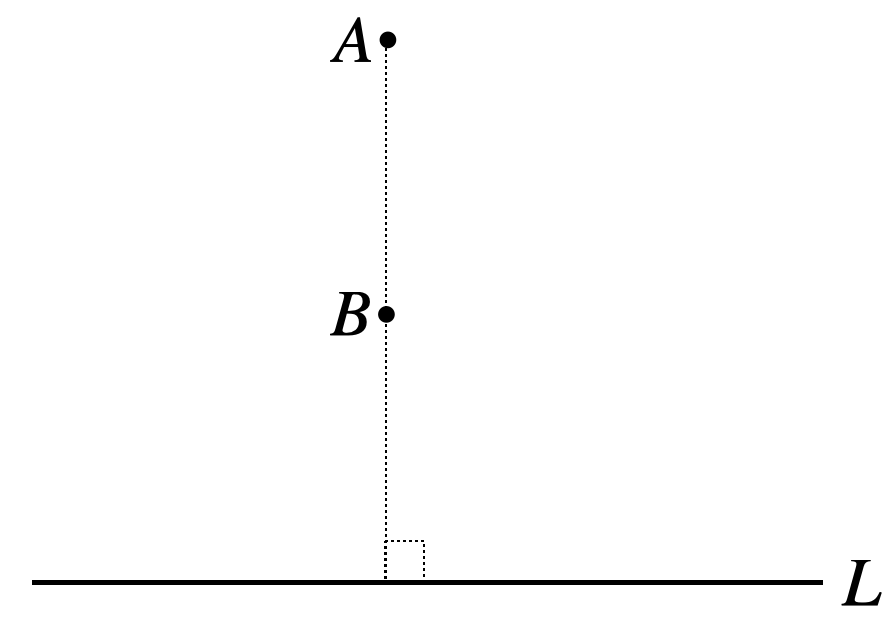
Fred starts running from point \(A\) and must reach point \(B\). On the way, he has to touch the fence shown as a straight line in the figure. It doesn’t matter where he touches the fence, as long as he does. What is the shortest path he can take?

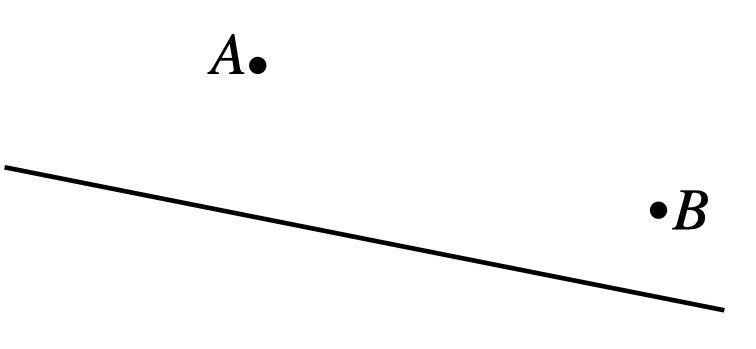
Robbie and Paloma are playing football on a large, flat field. They both run at the same speed toward the ball. Where could the ball have been if Paloma reached it first?

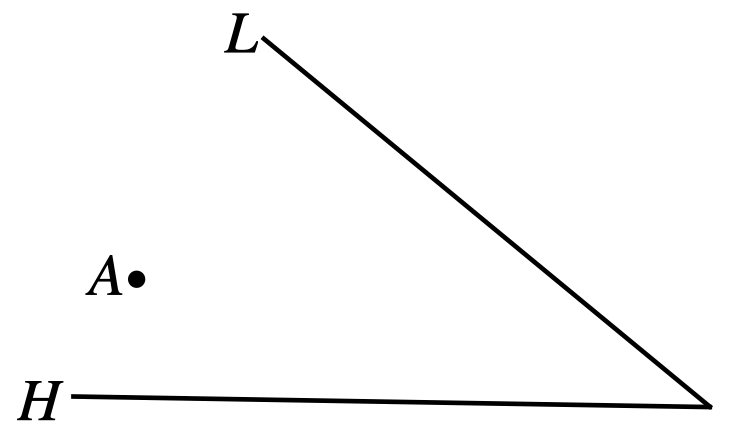
Oliver starts running from point \(A\) in the figure below. He must touch line \(H\), and then line \(L\). What is the shortest path he can take?

Two ants move along the same straight line and can only move back and forth along it. The first ant moves twice as fast as the second. Where could you place a breadcrumb so that the slower ant reaches it first?

Two ants, Muffy and Chip, start on opposite sides of a circle. Muffy moves twice as fast as Chip, and both can only move along the circle’s edge. Where could a breadcrumb be placed so that they both reach it at the same time?

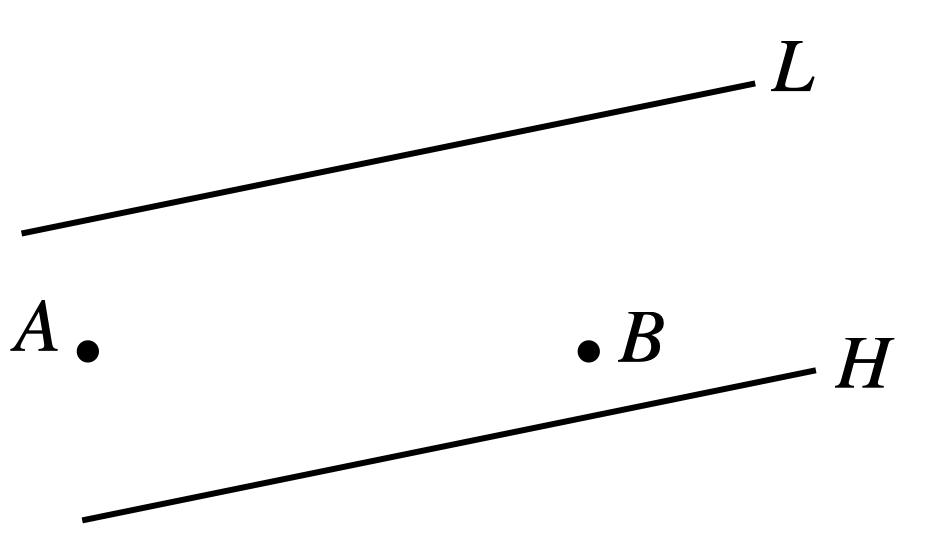
Two points, \(A\) and \(B\), lie between two lines \(L\) and \(H\). Draw the shortest path from \(A\) to \(B\) that touches \(L\), then \(H\), and finally reaches \(B\).

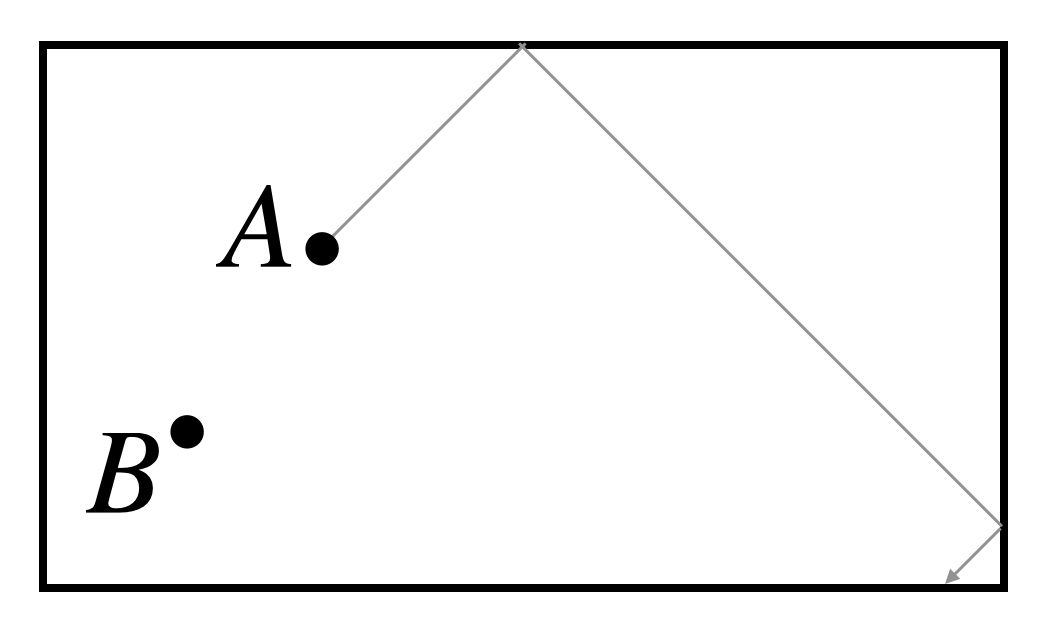
Ignat is playing pool and places a ball at point \(A\), as shown below. Can he bounce ball \(A\) off a ball placed at position \(B\), if the ball can only bounce off the top and right edges of the pool table?

When a ball bounces off the edge, it does so just like light reflecting in a mirror: the angle at which it hits the edge is the same as the angle at which it bounces away.

A ball \(A\) is placed on the pool table as shown below.

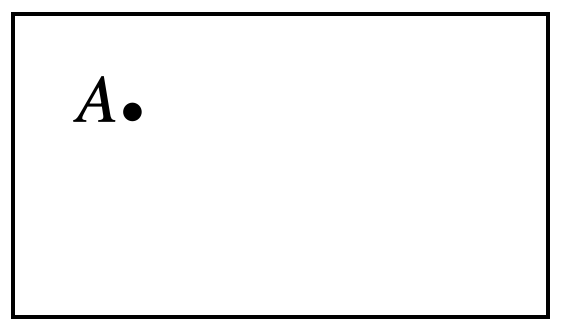
The walls are labeled as follows: wall \(1\) is the top wall, wall \(2\) is the right wall, wall \(3\) is the bottom wall, and wall \(4\) is the left wall. If we hit the ball so that it bounces off the walls labeled \(1\), \(2\), \(3\), and \(4\) —in that order—and then stops rolling just before hitting the next wall, what region of the pool table can the ball reach? If the ball hits a corner, it also stops.

A ball enters a wedge \(ABC\), striking the wall at \(A\) with an angle \(\alpha\), as shown in the diagram below.

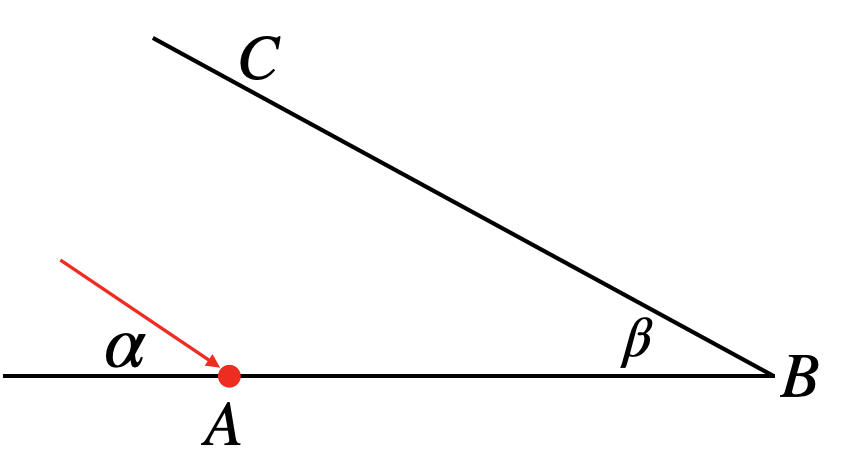
The wedge angle \(\angle ABC\) is \(\beta\). The ball keeps bouncing between the two walls until it eventually makes its last bounce (you can imagine that the sides \(AB\) and \(AC\) extend infinitely).

Find, in terms of \(\alpha\) and \(\beta\), how many times the ball bounces off the walls.

The roadrunner and the coyote start at points \(A\) and \(B\), respectively, as shown in the diagram below. The roadrunner’s goal is to reach the line \(L\), while the coyote aims to catch it before it gets there. First, the roadrunner chooses a direction and begins moving straight ahead, never changing its course. The coyote observes this direction and, immediately afterward, chooses its own direction and also moves straight ahead without turning. The roadrunner moves at twice the speed of the coyote, and once either begins moving, neither can stop. If the coyote eventually catches the roadrunner, where could they have met?