Problems
We want to prove Monsky’s theorem as a corollary of Sperner’s lemma:
it is not possible to dissect a square into an odd number of triangles
of equal area. After scaling we can consider the square with
coordinates: \((0,0),(0,1),(1,0),(1,1)\), which we want to
cut into \(n\) triangles with area
\(\frac{1}{n}\) each for an odd \(n\). Consider the following coloring of all
the points with rational coordinates \((\frac{p}{q},\frac{r}{s})\) inside the
square:
We look at the powers of \(2\) in the
fractions \((\frac{p}{q},\frac{r}{s})\), first of all
the numbers \(p,q\) are coprime, and
thus only one of them is divisible by \(2\), same with \(r,s\). Then the following possibilities
might occur:
Neither \(q\) nor \(s\) is divisible by \(2\). In this case we color the point red.
\(\frac{r}{s}\) is divisible by a larger or equal power of \(2\) than \(\frac{p}{q}\) and \(p\) is not divisible by \(2\). In this case we color the point blue.
\(\frac{p}{q}\) is divisible by a strictly larger power of \(2\) than \(\frac{r}{s}\) and \(r\) is not divisible by \(2\). In this case we color the point green.
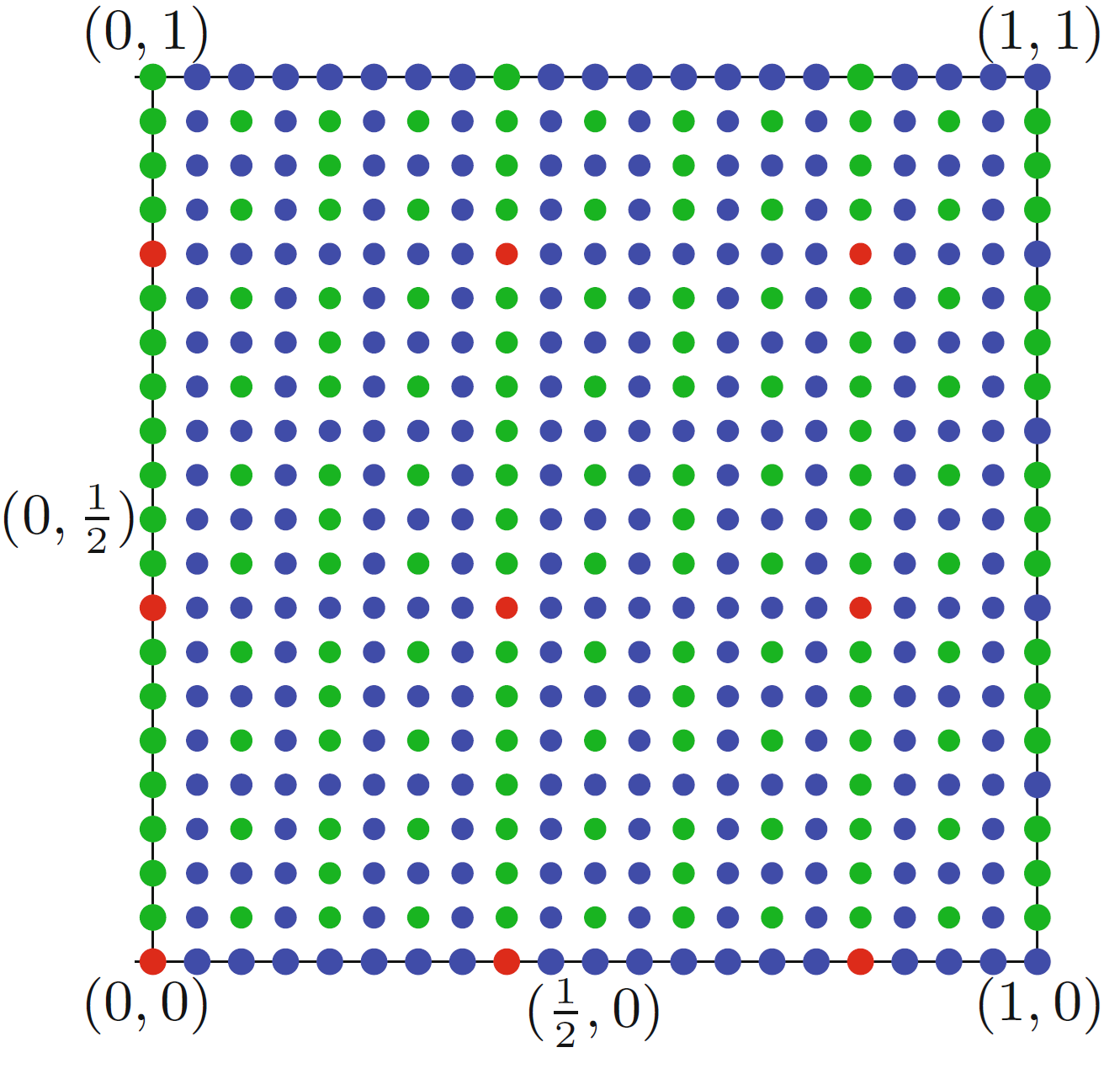
Under an assumption (which you do not have to prove) that the area of any rainbow triangle is at least \(\frac{1}{2}\) prove the Monsky’s theorem.
Prove the general version of Sperner’s lemma: Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\). Strictly speaking a simplex is a convex linear combination of \(n+1\) points in general position (when \(k\) points are never in one subspace of dimension \(k-1\)). One can view it as an \(n\)-dimensional tetrahedron or a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=1}^{n+1}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\]
A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells)
of the same dimension, such that any two cells are either disjoint, or
they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment
of \(n+1\) colors to the vertices of
the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors,
and points on each face of \(\mathcal{A}\) use only the colors of the
vertices defining the respective face of \(\mathcal{A}\).
Prove that every Sperner’s coloring of any subdivision of an \(n\)-dimensional simplex contains an odd
number of rainbow simplexes, namely whose vertices are colored using all
\(n+1\) colors.
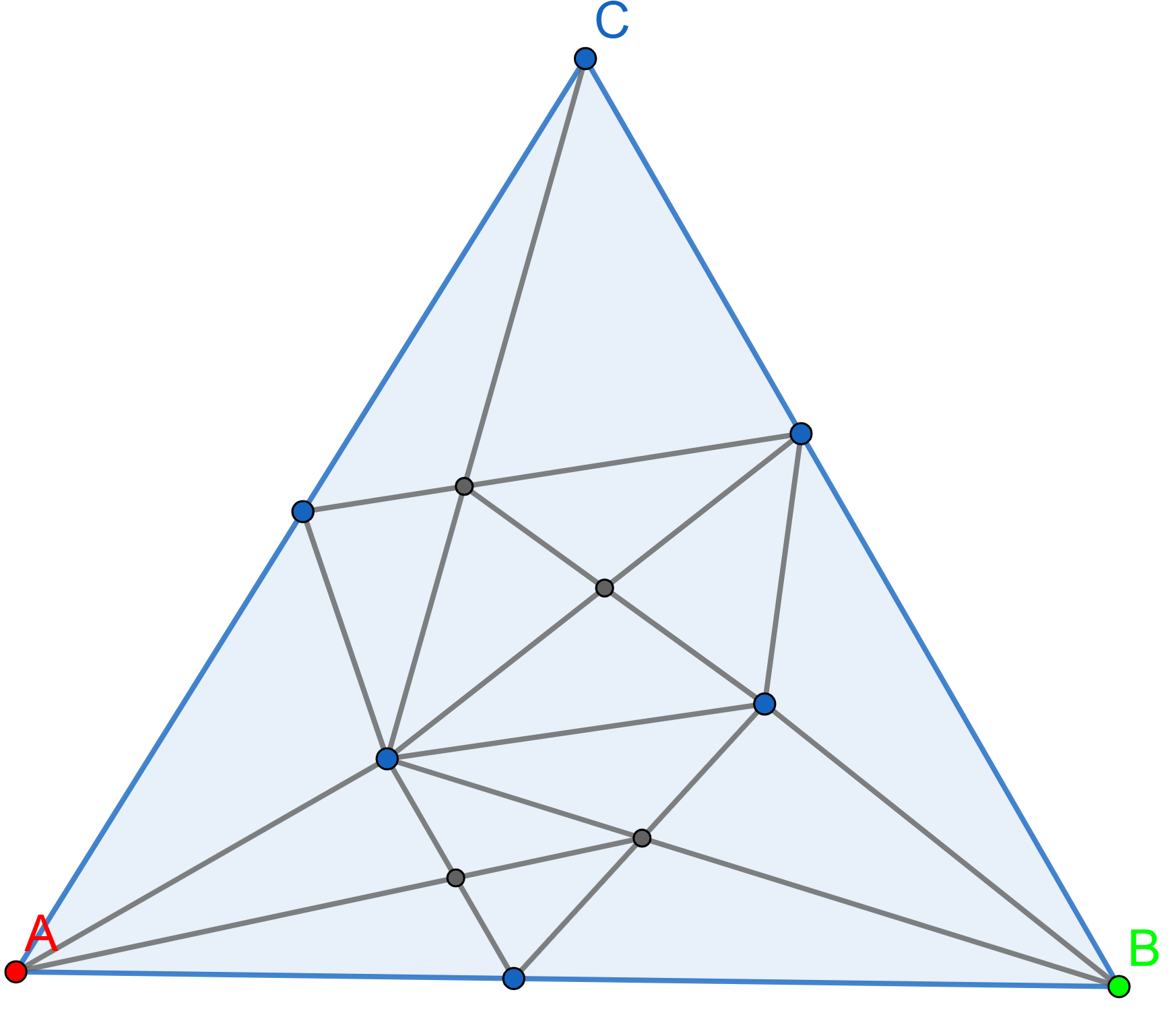
Draw Sperner’s coloring for the following triangulation. Try to avoid rainbow triangles at all costs.
Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\), namely a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=0}^{n}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\] Where next to \(a_i\) there is a point with coordinate where \(1\) is in \(i\)-th place. The point \((0,0,...,0)\) belongs to the simplex as well.
A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells)
of the same dimension, such that any two cells are either disjoint, or
they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment
of \(n+1\) colors to the vertices of
the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors,
and points on each face of \(\mathcal{A}\) use only the colors of the
vertices defining the respective face of \(\mathcal{A}\).
Consider a simplicial subdivision given by pairwise connected middles of
all the segments in the original simplex. Assign the numbers \(0,1,2...,n\) to the subdivision vertices in
such a way as to conduct a Sperner’s coloring in such a way that you
will have only one rainbow simplex.
Consider an equilateral triangle \(ABC\). Parallel to each side, five equally spaced segments are drawn across the triangle so that \(ABC\) is subdivided into \(36\) smaller equilateral triangles. Vertices \(A,B\) and \(C\) are painted red, blue and green, respectively in counterclockwise order. Alice and Bob take turns painting each vertex of the smaller triangles either red, green, or blue with the following restrictions: the segment \(AB\) can only have red or green, the segment \(BC\) can only have green and blue, and the segment \(AC\) can only have blue and red. The interior vertices can be drawn freely. Once all vertices have been painted, Alice gets a point for every smaller triangle whose vertices have the three colors (red, green, and blue) appearing in the counterclockwise direction. Bob gets a point for every smaller triangle whose vertices have the three colors but in the clockwise direction. Who wins?
There are \(100\) people in a room, and each person has at least one friend in the room. Prove that amongst them there are two people with the same number of friends in the room (we don’t count being friends with oneself).
Can we obtain the polynomial \(h(x)=x\) by adding, subtracting, or multiplying the polynomials \(f(x)=x^2+x\) and \(g(x)=x^2+2\)?
A cube net is a 2D shape that can be folded into a cube. For example, in the following diagram we show a cube net and the steps that fold it into a cube:
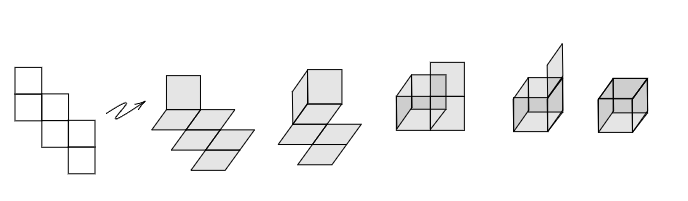
Imagine that you want to cover an endless floor with this cube net, so there are no gaps or overlaps, how would you lay them out? This is called covering or tiling the plane.
Cut a square into three parts and then use these three pieces to form a triangle such that:
All its angles are acute (i.e: less than \(90^\circ\)).
All its sides are of different lengths.
Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.