Problems

Can we obtain the polynomial \(h(x)=x\) by adding, subtracting, or multiplying the polynomials \(f(x)=x^2+x\) and \(g(x)=x^2+2\)?

A cube net is a 2D shape that can be folded into a cube. For example, in the following diagram we show a cube net and the steps that fold it into a cube:

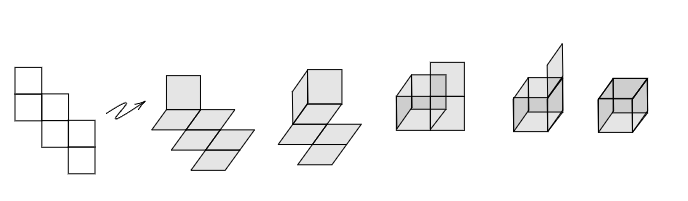
Imagine that you want to cover an endless floor with this cube net, so there are no gaps or overlaps, how would you lay them out? This is called covering or tiling the plane.

Cut a square into three parts and then use these three pieces to form a triangle such that:

1. All its angles are acute (i.e: less than \(90^\circ\)).

2. All its sides are of different lengths.

Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.

The Pythagorean Theorem is one of the most important facts about geometry. It says that if we have a right-angled triangle (i.e: it has an angle of \(90^\circ\)), whose longest side measures \(C\), and its other two other sides measure \(A\) and \(B\):

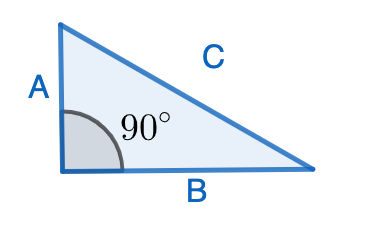
then \(A^2+B^2=C^2\). There are many proofs of this fact, and some involve dissections! Let’s have a look at the following two ways to dissect the same square:

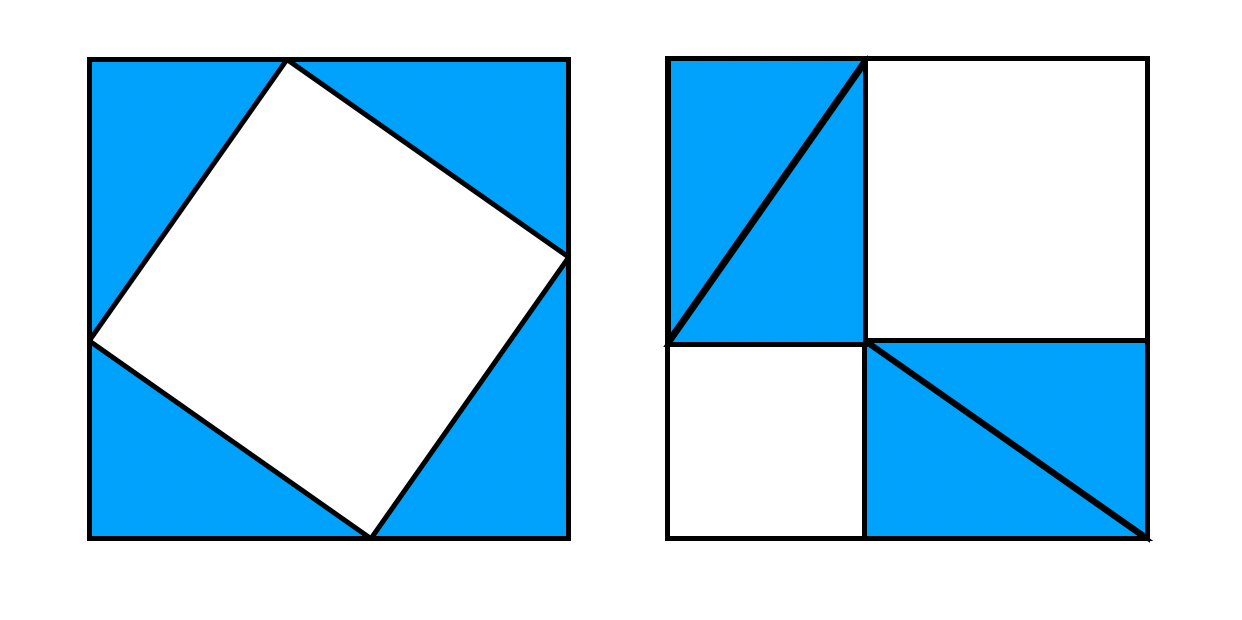
Can you explain how these dissections prove the Pythagorean Theorem?

Seven Smurfs live in seven mushroom houses. There is a tunnel between every pair of houses, so from any house you can walk to any other house. One of the Smurfs, Clumsy, starts walking from his house, but he must not use the same tunnel more than once. He keeps walking until he reaches a house where all the tunnels have already been used. Where will Clumsy’s journey end?

A battle of the captains was held at a maths battle. The task was to write the smallest number that is divisible by \(60\) and it’s digits are only ’\(1\)’s or ’\(0\)’s. What is the answer?

Suppose that \(x_1+y_1\sqrt{d}\) and \(x_2+y_2\sqrt{d}\) give solutions to Pell’s equation \(x^2-dy^2=1\) and \(x_1,x_2,y_1,y_2\geq 0\). Show that the following are equivalent:

1. \(x_1+y_1\sqrt{d} < x_2+y_2\sqrt{d}\),

2. \(x_1<x_2\) and \(y_1<y_2\),

3. \(x_1<x_2\) or \(y_1<y_2\).

If Pell’s equation \(x^2-dy^2 = 1\) has a nontrivial solution \((x_1,y_1)\), show that it has infinitely many distinct solutions.

Show that there are infinitely many triples of consecutive integers, each of which is a sum of the square of two integers.