Problems

If we glue the opposite sides of the paper band in the same direction as on the picture, we will get a cylinder. What surface do we get, if we glue the circles of the cylinder in the same direction as well?

We start with a rectangular sheet of paper - preferably with proportions more than \(6:1\), so that it looks more like a band. For now assume that one can stretch or shrink the paper band as needed. Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the opposite direction as in the picture.

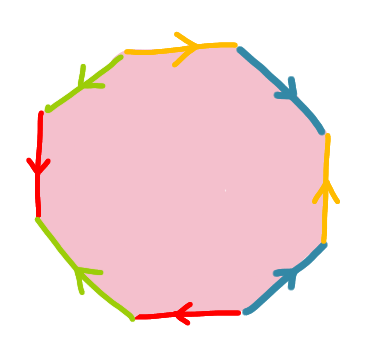
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.

Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.

Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.

Which of the following numbers are divisible by \(11\) and which are not? \[121,\, 143,\, 286, 235, \, 473,\, 798, \, 693,\, 576, \,748\] Can you write down and prove a divisibility rule which helps to determine if a three digit number is divisible by \(11\)?

In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?

An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.

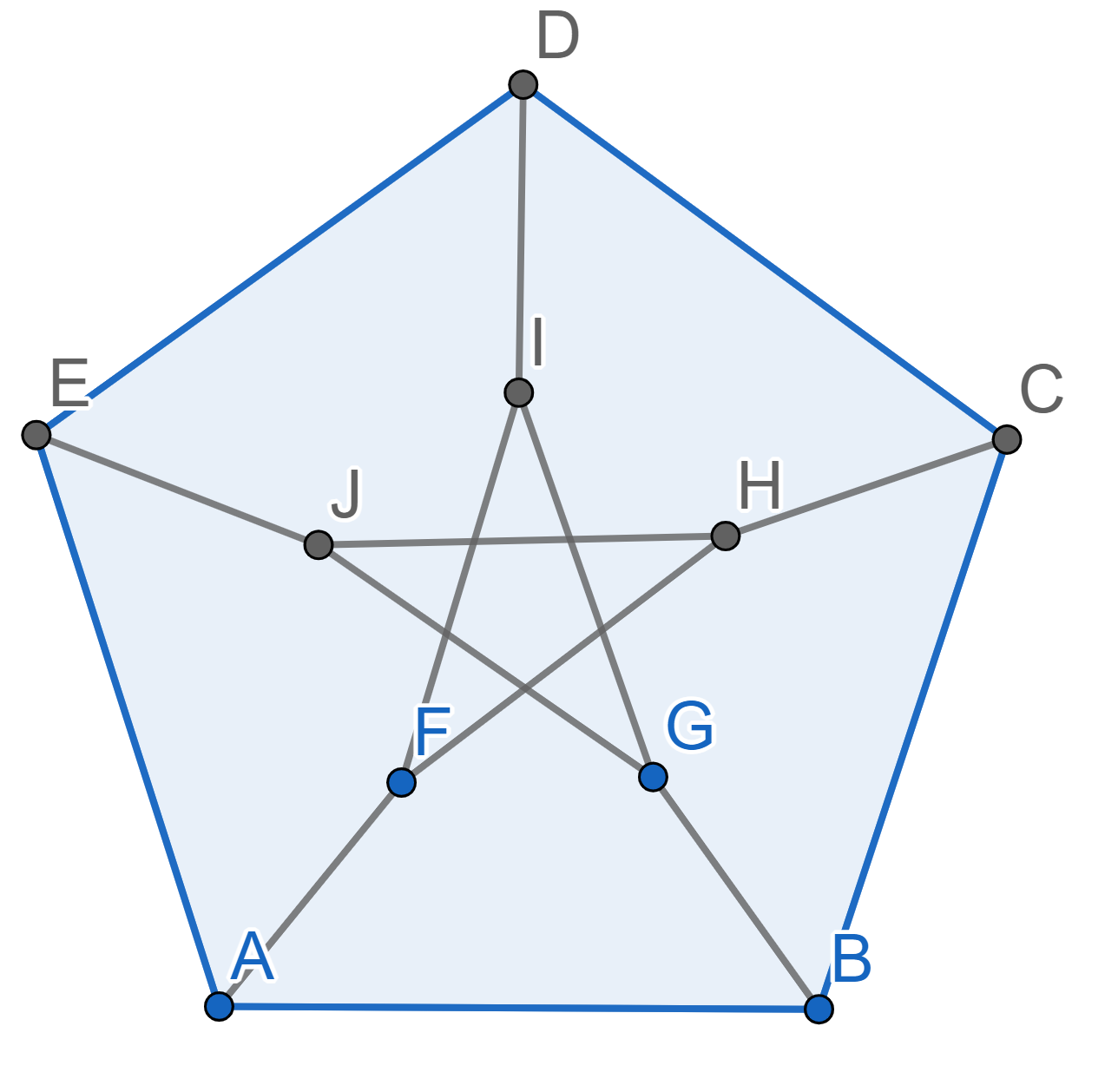
We wish to paint the \(15\) segments in the picture below in three colours. We want it such that no two segments of the same colour have a common end. For example, you cannot have both \(AB\) and \(BC\) blue since they share the end \(B\). Is such a painting possible?

A circle is inscribed into the triangle \(ABC\) with sides \(BC=6, AC=10\) and \(AB= 12\). A line tangent to the circle intersects two longer sides of the triangle \(AB\) and \(AC\) at the points \(F\) and \(G\) respectively. Find the perimeter of the triangle \(AFG\).

Liam saw an unusual clock in the museum: the clock had no digits, and it’s not clear how the clock should be rotated. That is, we know that \(1\) is the next digit clockwise from \(12\), \(2\) is the next digit clockwise from \(1\), and so on. Moreover all the arrows (hour, minute, and second) have the same length, so it’s not clear which is which. What time does the clock show?