Problems

Author: A.A. Egorov

Calculate the square root of the number \(0.111 \dots 111\) (100 ones) to within a) 100; b) 101; c)* 200 decimal places.

Two lines on the plane intersect at an angle \(\alpha\). On one of them there is a flea. Every second it jumps from one line to the other (the point of intersection is considered to belong to both straight lines). It is known that the length of each of her jumps is 1 and that she never returns to the place where she was a second ago. After some time, the flea returned to its original point. Prove that for the angle \(\alpha\) the value \(\alpha/\pi\) is a rational number.

In some country there are 101 cities, and some of them are connected by roads. However, every two cities are connected by exactly one path.

How many roads are there in this country?

a) The vertices (corners) in a regular polygon with 10 sides are colored black and white in an alternating fashion (i.e. one vertex is black, the next is white, etc). Two people play the following game. Each player in turn draws a line connecting two vertices of the same color. These lines must not have common vertices (i.e. must not begin or end on the same dot as another line) with the lines already drawn. The winner of the game is the player who made the final move. Which player, the first or the second, would win if the right strategy is used?

b) The same problem, but for a regular polygon with 12 sides.

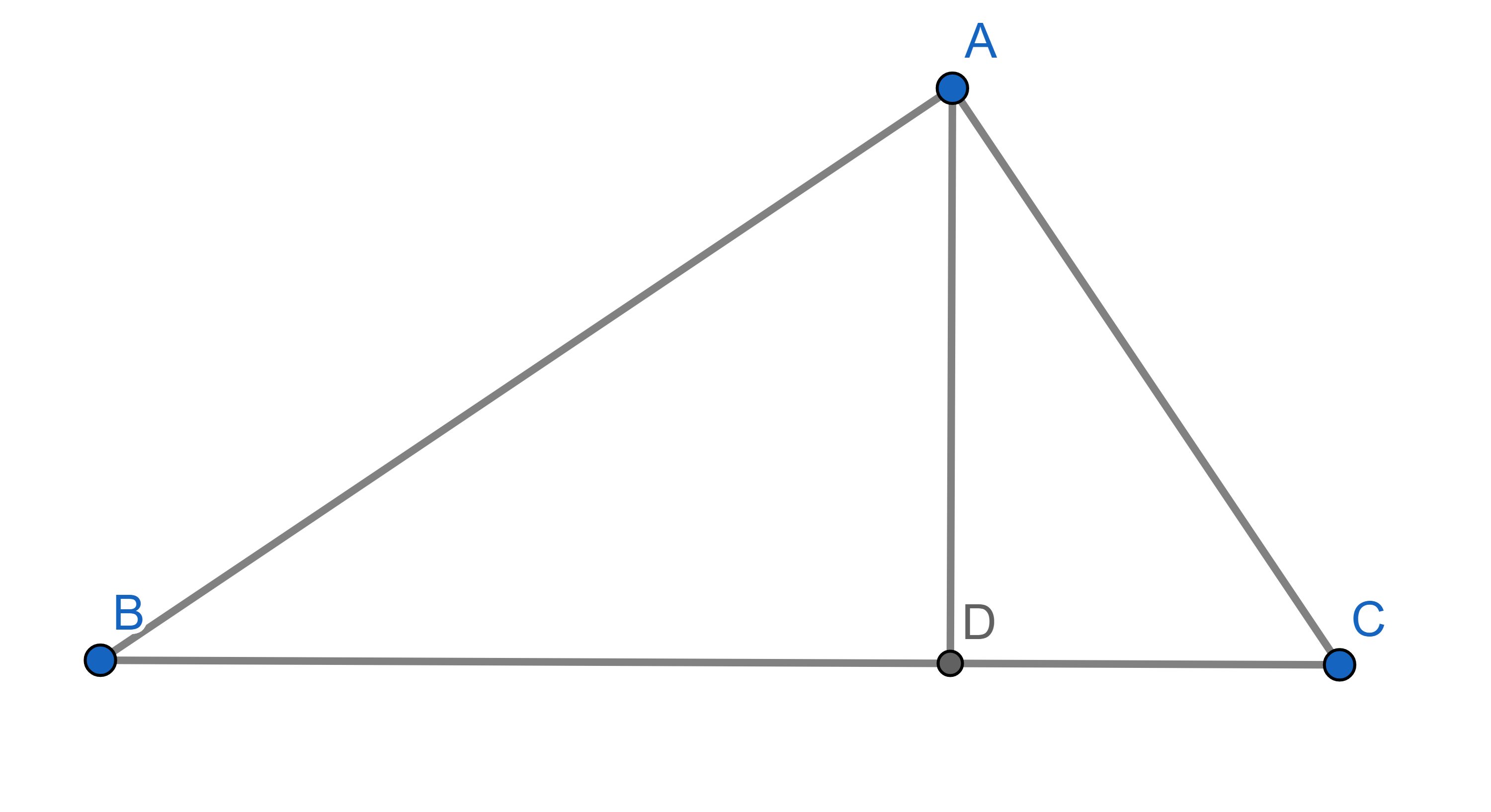
Matt built a simple wooden hut to protect himself from the rain. From the side the hut looks like a right triangle with the right angle at the top. The longer part of the roof has \(20\) ft and the shorter one has \(15\) ft. What is the height of the hut in feet?

On the first day Robinson Crusoe tied the goat with a piece of rope by putting one peg into the ground. What shape did the goat graze?

On the second day Robinson Crusoe stretched the rope between two pegs, put a ring on the rope, and tied the goat with another rope to the ring. What shape did the goat graze in this case?

On the third day Robinson Crusoe put two pegs again, and decided not to stretch the rope, but to tie the goat with two loose ropes of different lengths to those pegs. What shape did the goat graze on the third day?

One day Robinson Crusoe decided to take his usual walk, and followed his path on a plateau holding his goat on the lead of 1 m length. Draw the shape of the area where the goat could have being eating grass while walking along Robinson Crusoe. The path they followed was exactly in the shape of 1 km\({}\times{}\)3 km rectangle.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a semicircle