Problems
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:
The figure below is a regular pentagram. What is larger, the black area or the blue area?
A circle was inscribed in a square, and another square was inscribed in the circle. Which area is larger, the blue or the orange one?
In a square, the midpoints of its sides were marked and some segments were drawn. There is another square formed in the centre. Find its area, if the side of the square has length \(10\).
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(AB\), point \(F\) belongs to the side \(CD\) and point \(G\) belongs to the side \(AD\). What is more, the marked red segments \(AE\) and \(CF\) have equal lengths. Prove that the total grey area is equal to the total black area.
Matt built a simple wooden hut to protect himself from the rain. From the side the hut looks like a right triangle with the right angle at the top. The longer part of the roof has 20 ft and the shorter one has 15 ft. What is the height of the hut in feet?
The three sides of a right triangle have all integer lengths. Show that at least one of them has an even length.
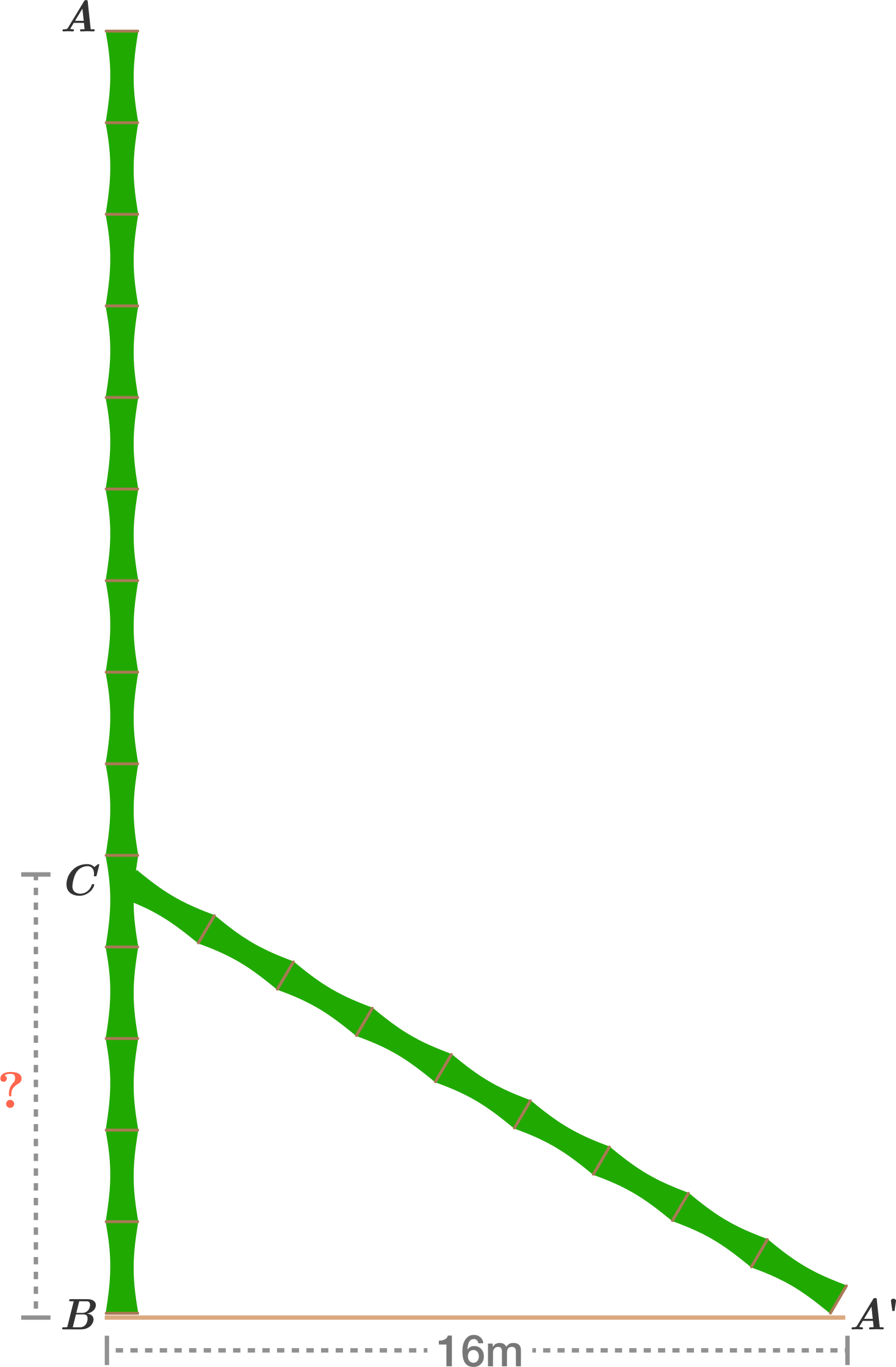
A bamboo tree, originally \(32\) metres high, broke in two parts. The end of the other one has fallen \(16\) metres away from the trunk. How high is the remaining vertical part of the bamboo tree?
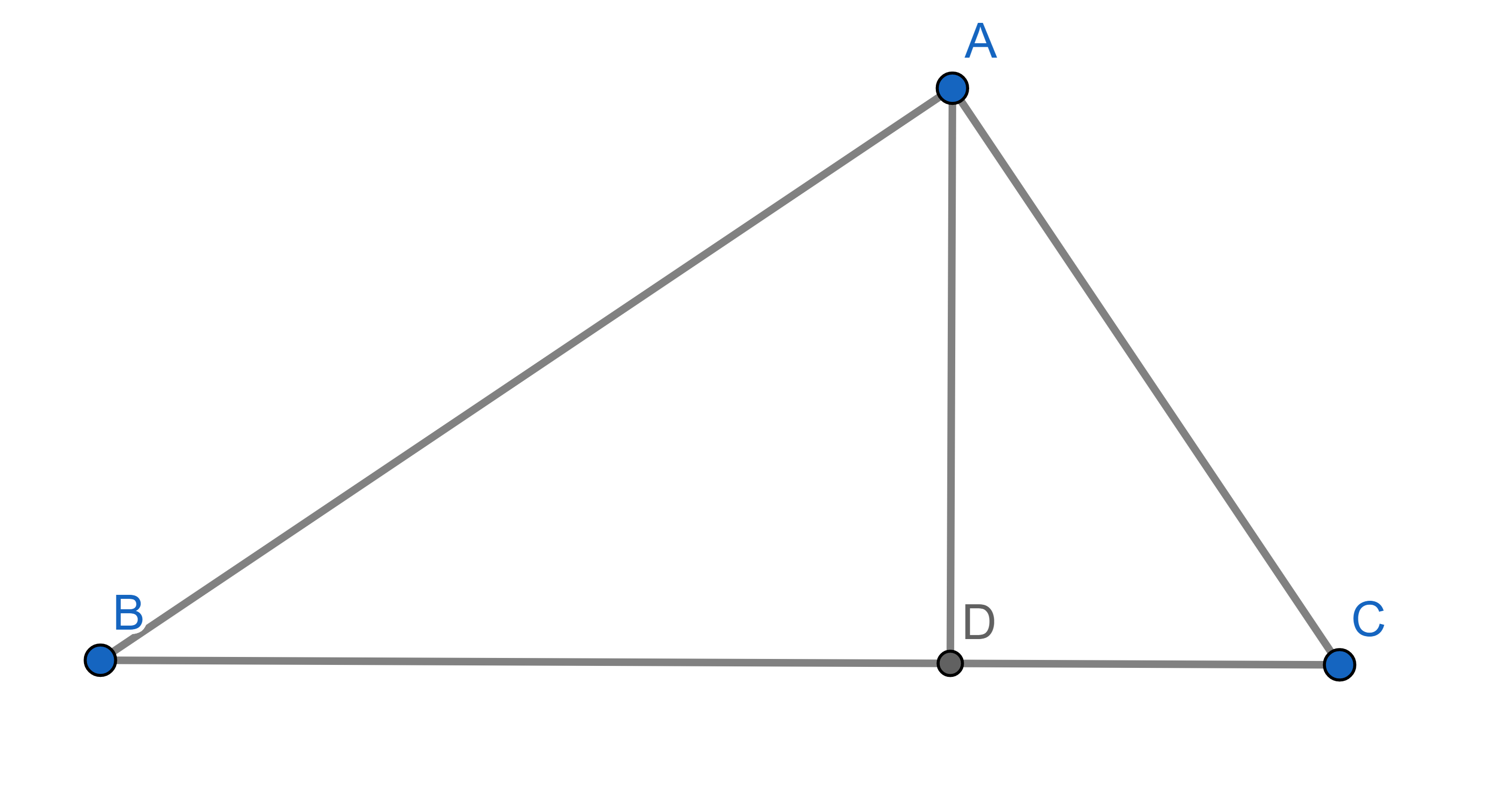
Matt has built an additional support for his hut (\(AD\)), whose length is \(12\)ft, and the base \(BC\) is \(25\)ft. We also know \(AB = 20\) and \(AC = 15\). What are the distances \(|BD|\) and \(|DC|\)? Show that \(|AD|^2=|BD| \times |AC|\) in this particular case. Do you think it is true in general?
Can you build a right-angled triangle using 25 identical matches without breaking them? You have to use them all. If yes, show how. If not, show why.