Problems

A billiard ball lies on a table in the shape of an acute angle. How should you hit the ball so that it returns to its starting location after hitting each of the two banks once? Is it always possible to do so?
(When the ball hits the bank, it bounces. The way it bounces is determined by the shortest path rule – if it begins at some point \(D\) and ends at some point \(D'\) after bouncing, the path it takes is the shortest possible path that includes the bounce.)

In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:

The figure below is a regular pentagram. What is larger, the black area or the blue area?

A circle was inscribed in a square, and another square was inscribed in the circle. Which area is larger, the blue or the orange one?

In a square, the midpoints of its sides were marked and some segments were drawn. There is another square formed in the centre. Find its area, if the side of the square has length \(10\).

In a parallelogram \(ABCD\), point \(E\) belongs to the side \(AB\), point \(F\) belongs to the side \(CD\) and point \(G\) belongs to the side \(AD\). What is more, the marked red segments \(AE\) and \(CF\) have equal lengths. Prove that the total grey area is equal to the total black area.

Construct a triangle with the side \(c\), median to side \(a\), \(m_a\), and median to side \(b\), \(m_b\).

Construct a triangle with the side \(a\), the side \(b\) and height to side \(a\), \(h_a\).

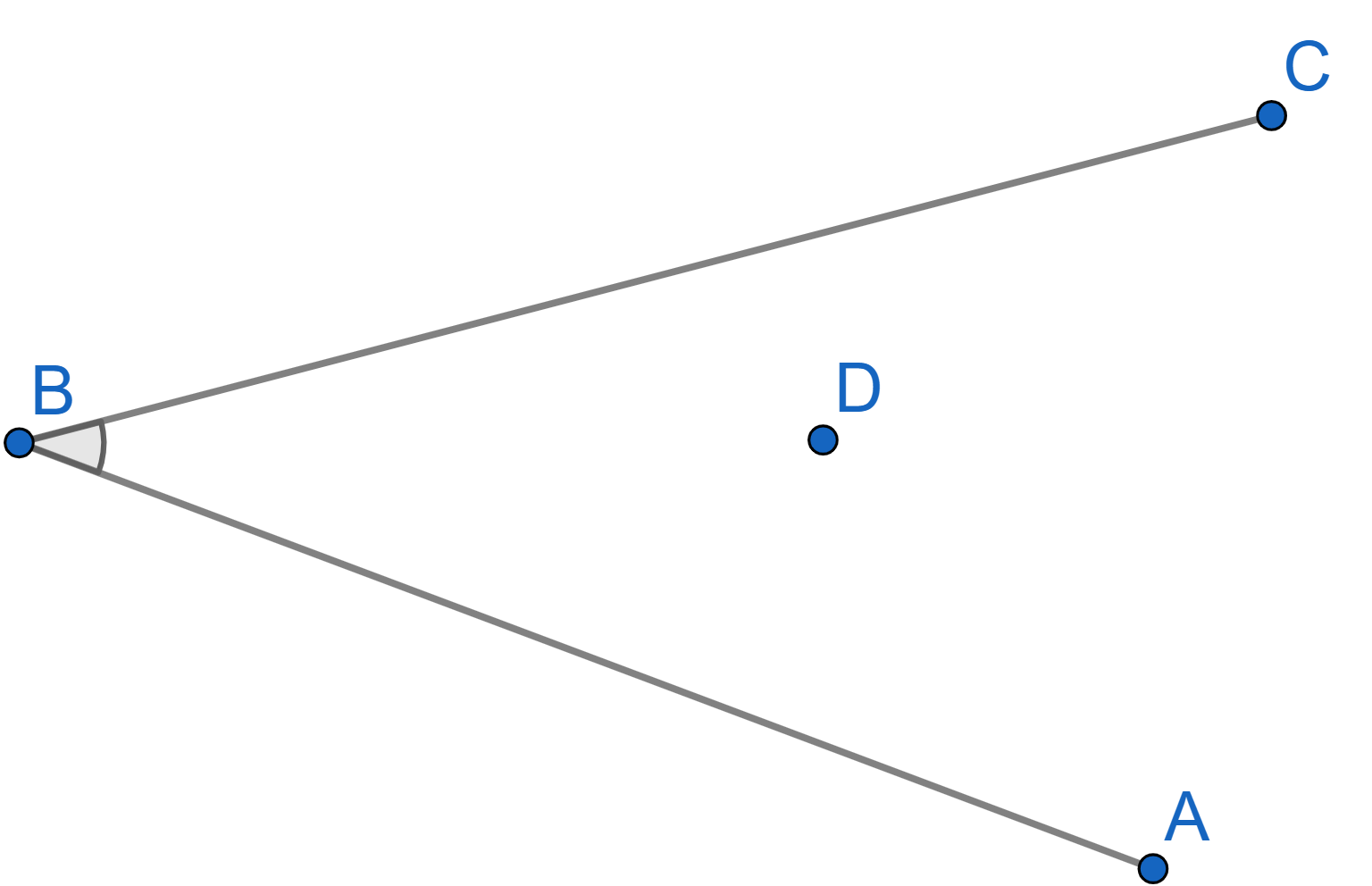
Inside an angle two points, \(A\) and \(B\), are given. Construct a circle which passes through these points and cuts the sides of the angle into equal segments.

Two segments \(AB\) and \(A'B'\) are given on a plane. Construct the point \(O\) so that the triangles \(AOB\) and \(A'OB'\) are similar (the same letters denote the corresponding vertices of similar triangles).