Problems
In the first term of the year Daniel received five grades in mathematics with each of them being on a scale of 1 to 5, and the most common grade among them was a 5 . In this case it turned out that the median of all his grades was 4, and the arithmetic mean was 3.8. What grades could Daniel have?
A sailor can only serve on a submarine if their height does not exceed 168 cm. There are four teams \(A\), \(B\), \(C\) and \(D\). All sailors in these teams want to serve on a submarine and have been rigorously selected. There remains the last selection round – for height.
In team \(A\), the average height of sailors is 166 cm.
In team \(B\), the median height of the sailors is 167 cm.
In team \(C\), the tallest sailor has a height of 169 cm.
In team \(D\), the mode of the height of the sailors is 167 cm.
In which team, can at least half of the sailors definitely serve on the submarine?
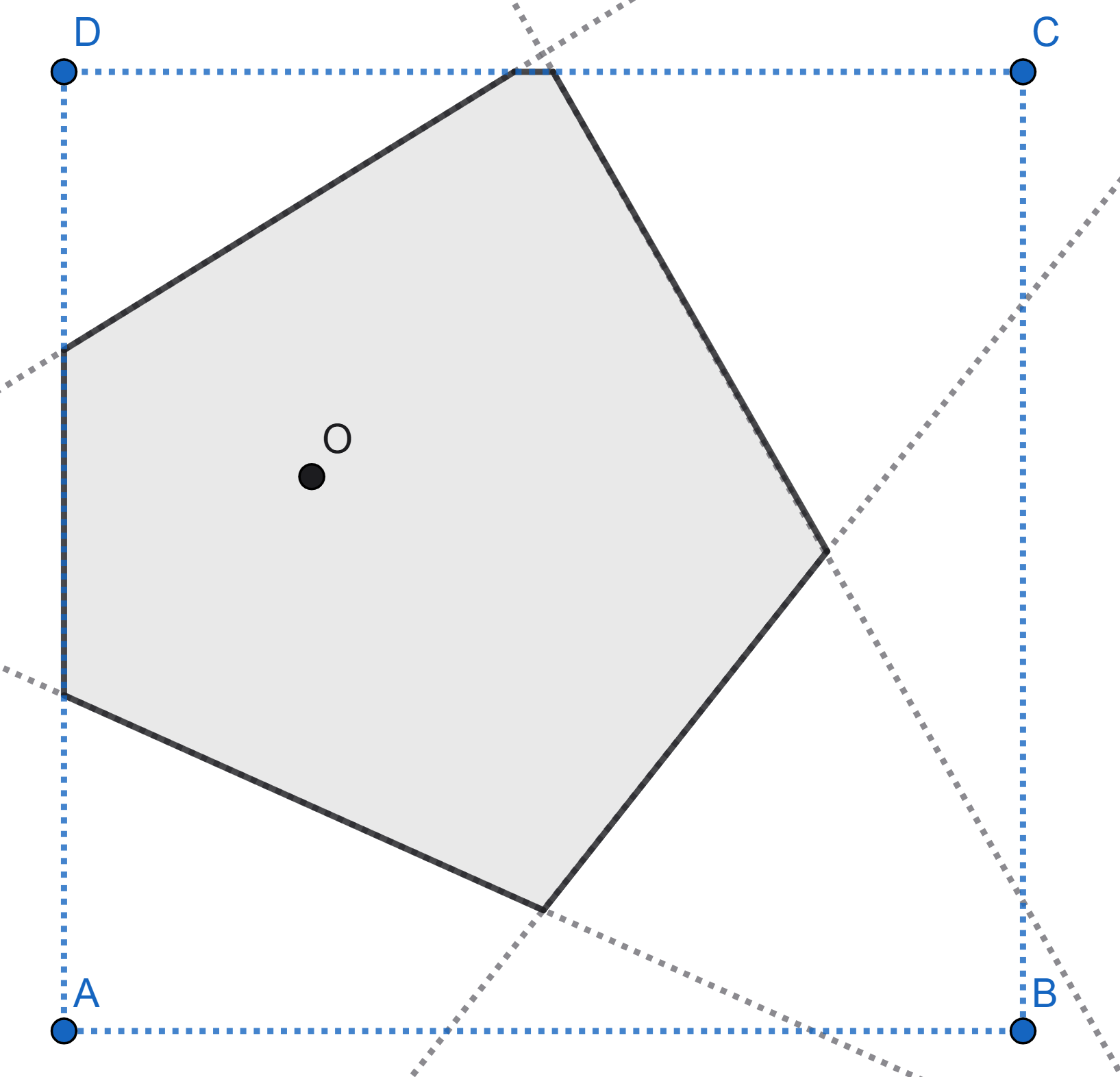
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.
The bus has \(n\) seats, and all of the tickets are sold to \(n\) passengers. The first to enter the bus is the Scattered Scientist and, without looking at his ticket, takes a random available seat. Following this, the passengers enter one by one. If the new passenger sees that his place is free, he takes his place. If the place is occupied, then the person who gets on the bus takes the first available seat. Find the probability that the passenger who got on the bus last will take his seat according to his ticket?
The point \(O\), lying inside the triangle \(ABC\), is connected by segments with the vertices of the triangle. Prove that the variance of the set of angles \(AOB\), \(AOC\) and \(BOC\) is less than a) \(10\pi ^2/27\); b) \(2\pi ^2/9\).
Valerie wrote the number 1 on the board, and then several more numbers. As soon as Valerie writes the next number, Mike calculates the median of the already available set of numbers and writes it in his notebook. At some point, in Mike’s notebook, the numbers: 1; 2; 3; 2.5; 3; 2.5; 2; 2; 2; 2.5 are written.
a) What is the fourth number written on the board?
b) What is the eighth number written on the board?
On a laundry drying line \(n\) socks hang in a random order (the order in which they got out of the washing machine). Among them there are the two favourite socks of the Scattered Scientist. The socks are covered by a drying sheet, so the Scientist does not see them, and takes out one sock by touch. Find the mathematical expectation of the number of socks taken out by the Scientist by the time he has both of his favourite socks.
An ant goes out of the origin along a line and makes \(a\) steps of one unit to the right, \(b\) steps of one unit to the left in some order, where \(a > b\). The wandering span of the ant is the difference between the largest and smallest coordinates of the ant for the entire length of its journey.
a) Find the largest possible wandering range.
b) Find the smallest possible range.
c) How many different sequences of motion of the ant are there, where the wandering range is the greatest possible?
In Anchuria, presidential elections are being prepared, in which President Miraflores wants to win. Exactly half of the voters support Miraflores, and the other half support Dick Maloney. Miraflores is also a voter. According to the law, he has the right to divide all of the voters into two constituencies at his own discretion. In each of the districts, the voting is conducted as follows: each voter marks the name of their candidate on the ballot; all ballots are placed in the ballot box. Then one random ballot is chosen from the ballot box, and the one whose name is marked on it will win in this district. The candidate wins the election only if he wins in both districts. If the winner does not appear, the next round of voting is appointed according to the same rules. How should Miraflores divide the electorate in order to maximize the probability of his victory on the first round?
In a terrible thunderstorm, along a rope ladder, \(n\) dwarfs ascend in a chain. If suddenly there is a thunderbolt, then from fear, every gnome, regardless of others, can fall with probability \(p\) (\(0 < p < 1\)). If the dwarf falls, then he also hits all of the dwarfs that are below him. Find:
a) The probability that exactly \(k\) dwarfs will fall.
b) The mathematical expectation of the number of fallen dwarfs.