Problems

A class contains 38 pupils. Prove that within the class there will be at least 4 pupils born in the same month.

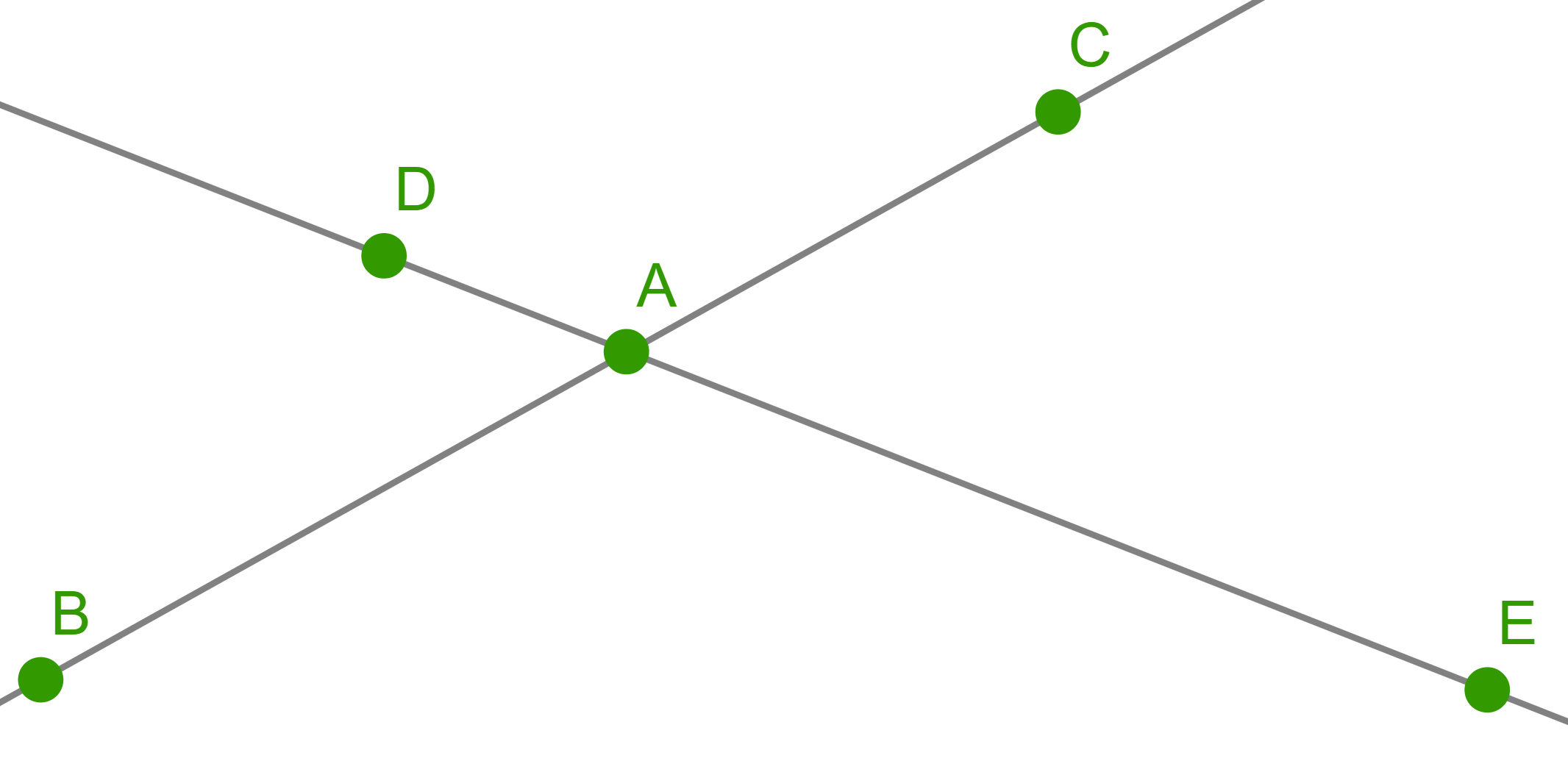
Five oaks are planted along two linear park alleys in such a way that there are three oaks along each alley, see picture. Where should we plant the sixth oak so that it will be possible to lay two more linear alleys, along each of which there would also be three oak trees growing?

The smell of a flowering lavender plant diffuses through a radius of 20 m around it. How many lavender plants must be planted along a straight 400m path so that the smell of the lavender reaches every point on the path.

Given an endless piece of chequered paper with a cell side equal to one. The distance between two cells is the length of the shortest path parallel to cell lines from one cell to the other (it is considered the path of the center of a rook). What is the smallest number of colors to paint the board (each cell is painted with one color), so that two cells, located at a distance of 6, are always painted with different colors?

A group of numbers \(A_1, A_2, \dots , A_{100}\) is created by somehow re-arranging the numbers \(1, 2, \dots , 100\).

100 numbers are created as follows: \[B_1=A_1,\ B_2=A_1+A_2,\ B_3=A_1+A_2+A_3,\ \dots ,\ B_{100} = A_1+A_2+A_3\dots +A_{100}.\]

Prove that there will always be at least 11 different remainders when dividing the numbers \(B_1, B_2, \dots , B_{100}\) by 100.

Prove that in any group of 7 natural numbers – not necessarily consecutive – it is possible to choose three numbers such that their sum is divisible by 3.

a) We are given two cogs, each with 14 teeth. They are placed on top of one another, so that their teeth are in line with one another and their projection looks like a single cog. After this 4 teeth are removed from each cog, the same 4 teeth on each one. Is it always then possible to rotate one of the cogs with respect to the other so that the projection of the two partially toothless cogs appears as a single complete cog? The cogs can be rotated in the same plane, but cannot be flipped over.

b) The same question, but this time two cogs of 13 teeth each from which 4 are again removed?

We are given 101 rectangles with integer-length sides that do not exceed 100.

Prove that amongst them there will be three rectangles \(A, B, C\), which will fit completely inside one another so that \(A \subset B \subset C\).

A staircase has 100 steps. Vivian wants to go down the stairs, starting from the top, and she can only do so by jumping down and then up, down and then up, and so on. The jumps can be of three types – six steps (jumping over five to land on the sixth), seven steps or eight steps. Note that Vivian does not jump onto the same step twice. Will she be able to go down the stairs?

10 friends sent one another greetings cards; each sent 5 cards. Prove that there will be two friends who sent cards to one another.