Problems

King Hattius has \(n\) prisoners, when \(n\ge4\) is a positive integer, and is feeling generous since his court of Logicians did well at his daughter’s logic puzzle. This means he offers the prisoners a puzzle, and he’ll let them all free if at least one of them is correct.

He has lots of hats, coming in \(n\) different colours. He tells the prisoners that he’ll put a hat on each of their heads. They might all have different coloured hats, or some of the hat’s colours could be the same. The king tells them that they can see everyone else’s hat colour, but not their own, and that they’re not allowed to communicate once their hats are on. They all have to simultaneously guess the colour of their hat.

He does give them the chance to come up with a strategy before he puts their hats on. How would you help the prisoners escape?

Pascal and Pierre are trying to work out Pythagoras. Being a bit obnoxious, Pythagoras puts a list of \(10\) possible dates on the table in front of them. In private, Pythag tells Pascal only the month of his birthday, and Pierre only the day of the month.

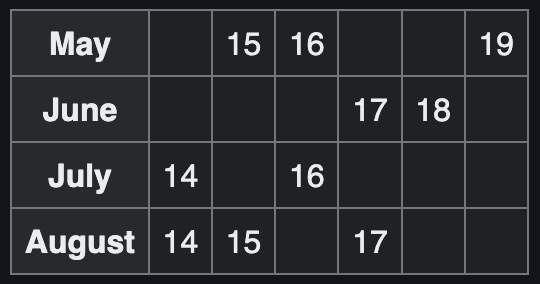
Pascal says “I don’t know Pythagoras’ birthday, but I also know that Pierre doesn’t know."
Pierre then says “Pascal was right that I didn’t know, but now I do know." Pascal replies “I know now Pythagoras’ birthday."

What is Pythagoras’ birthday?

Ignat gives two tutors a problem. He’s thinking of two different positive integers greater than \(1\), whose sum is at most \(100\). Ignat tells Pier (\(P\)) the product of the two numbers, and Sasha (\(S\)) the sum of the two numbers. Both Pier and Sasha know all of this, and then have a little conversation:

Sasha says that Pier doesn’t know the two numbers.

Pier says that he knows the two numbers.

Finally Sasha says that he knows the two numbers.
What are the two numbers?

On a bus out of the Hattius kingdom, you sit behind two wizards. The first says to the second “I’ve a positive integer number of children, all of whose ages are positive integers. The sum of their ages is the bus number, and their product is my age."

The second wizard replies “If you told me your age and how many children you had, would I be able to work out their individual ages?"

The first wizard says “No, unfortunately not." To which the second says “Aha! Now I know how old you are." What was the bus number?

Eleven sages were blindfolded and on everyone’s head a cap of one of \(1000\) colours was put. After that their eyes were untied and everyone could see all the caps except for their own. Then at the same time everyone shows the others one of the two cards – white or black. After that, everyone must simultaneously name the colour of their caps. Will they succeed?

The recertification of the Council of Sages takes place as follows: the king arranges them in a column one by one and puts on a cap of white or black colours for each. All the sages see the colours of all the caps of the sages standing in front, but they do not see the colour of their own and all those standing behind. Once a minute one of the wise men must shout one of the two colours. (each sage shouts out a colour once). After the end of this process the king executes every sage who shouts a colour different from the colour of his cap. On the eve of the recertification all one hundred members of the Council of Sages agreed and figured out how to minimize the number of those executed. How many of them are guaranteed to avoid execution?

At the elections to the High Government every voter who comes, votes for himself (if he is a candidate) and for those candidates who are his friends. The forecast of the media service of the mayor’s office is considered good if it correctly predicts the number of votes at least for one of the candidates, and not considered good otherwise. Prove that for any forecast voters can show up at the elections in such a way that this forecast will not be considered good.