Problems
Which five-digit numbers are there more of: ones that are not divisible by 5 or those with neither the first nor the second digit on the left being a five?
Alex laid out an example of an addition of numbers from cards with numbers on them and then swapped two cards. As you can see, the equality has been violated. Which cards did Alex rearrange?
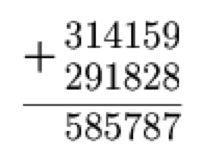
Solve the problem: \(AX \times UX = 2001\). Both \(X\) stand for the same digit, but \(A\), \(U\) and \(X\) are all different single digits.
The number \(A\) is positive, \(B\) is negative, and \(C\) is zero. What is the sign of the number \(AB + AC + BC\)?
a) A 1 or a 0 is placed on each vertex of a cube. The sum of the 4 adjacent vertices is written on each face of the cube. Is it possible for each of the numbers written on the faces to be different?
b) The same question, but if 1 and \(-1\) are used instead.
At the end of the term, Billy wrote out his current singing marks in a row and put a multiplication sign between some of them. The product of the resulting numbers turned out to be equal to 2007. What is Billy’s term mark for singing? (The marks that he can get are between 2 and 5, where 5 is the highest mark).
Is it possible to arrange the numbers 1, 2, ..., 60 in a circle in such an order that the sum of every two numbers, between which lies one number, is divisible by 2, the sum of every two numbers between which lie two numbers, is divisible by 3, the sum of every two numbers between which lie six numbers, is divisible by 7?
Pinocchio correctly solved a problem, but stained his notebook. \[(\bullet \bullet + \bullet \bullet+1)\times \bullet= \bullet \bullet \bullet\]
Under each blot lies the same number, which is not equal to zero. Find this number.
Four people discussed the answer to a task.
Harry said: “This is the number 9”.
Ben: “This is a prime number.”
Katie: “This is an even number.”
And Natasha said that this number is divisible by 15.
One boy and one girl answered correctly, and the other two made a mistake. What is the actual answer to the question?
Peter recorded an example of an addition on a board, after which he replaced some digits with letters, with the same figures being replaced with the same letters, and different figures with different letters. He did it such that he was left with the sum: \(CROSS + 2011 = START\). Prove that Peter made a mistake.