Problems

Age
Difficulty
 Clear filters
Found: 190
Problem #PRU-102989
 10–12  2.0

In a bookcase, there are four volumes of the collected works of Astrid Lindgren, with each volume containing 200 pages. A worm who lives on this bookshelf has gnawed its way from the first page of the first volume to the last page of the fourth volume. Through how many pages has the worm gnawed its way through?

Problem #PRU-102998
 10–12  2.0

Can the equality \(K \times O \times T = U \times W \times E \times N \times H \times Y\) be true if the numbers from 1 to 9 are substituted for the letters? Different letters correspond to different numbers.

Problem #PRU-103781
 11–12  2.0

A pedestrian walked along six streets of one city, passing each street exactly twice, but could not get around them, having passed each one only once. Could this be?

Problem #PRU-103800
 10–12  2.0

In two purses lie two coins, and one purse has twice as many coins as the other. How can this be?

Problem #PRU-103815
 11–11  2.0

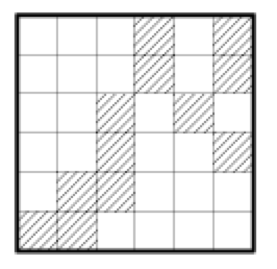
Cut the board shown in the figure into four congruent parts so that each of them contains three shaded cells. Where the shaded cells are placed in each part need not be the same.
image

Problem #PRU-104037
 11–13  2.0

Gerard says: the day before yesterday I was 10 years old, and next year I will turn 13. Can this be?

Problem #PRU-104039
 12–14  2.0

We call a natural number “amazing” if it has the form \(a^b + b^a\) (where \(a\) and \(b\) are natural numbers). For example, the number 57 is amazing, since \(57 = 2^5 + 5^2\). Is the number 2006 amazing?

Problem #PRU-104041
 12–13  2.0

Homework. Cut a hole in an exercise book of a size so that you yourself can climb through it.

Problem #PRU-104045
 12–13  2.0

a) In how many ways can Dima paint five Christmas trees in silver, green and blue colours, if the amount of paint is unlimited, and he paints each tree in only one colour?

b) Dima has five baubles: a red, a green, a yellow, a blue and a gold one. In how many ways can he decorate five Christmas trees with them, if he needs to put exactly one bauble on each tree?

c) What about if he can hang several baubles on one Christmas tree (and all of the baubles have to be used)?

Problem #PRU-104122
 12–13  2.0

Henry did not manage to get into the elevator on the first floor of the building and decided to go up the stairs. It takes 2 minutes to rise to the third floor. How long does it take to rise to the ninth floor?