Problems

Show how five queens can dominate a standard \(8\times8\) chessboard. That is, each square is attacked by some queen.

How many independent queens can you place on a \(5\times5\) grid? That is, so none of them attack each other.

How many ways can you place \(8\) rooks independently on a chessboard? That is, so that none of them attack each other.

Why are there no closed knight’s tours on an \(n\times n\) grid when \(n\) is odd? A knight’s tour is closed if you can get to the first square from the last square by a knight’s move.

Show how to place fourteen dominating bishops on a standard \(8\times8\) chessboard. That is, every square either contains a bishop, or is attacked by some bishop.

Place eight independent queens on a standard \(8\times8\) chessboard.

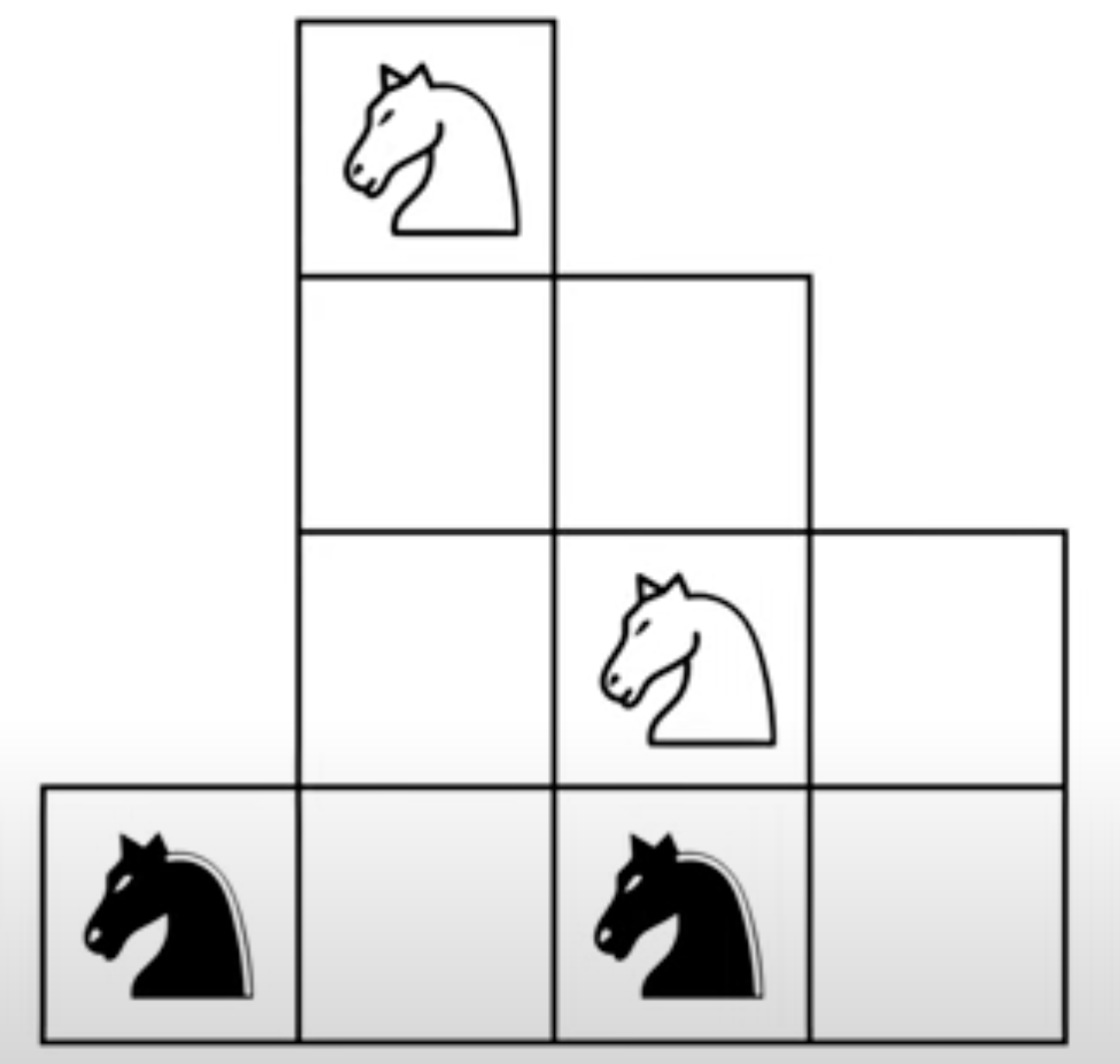
Show how to swap the two pairs of knights on the following strangely-shaped grid. That is, the knights make one move at a time, and you’re trying to get the black nights to where the white knights are, and the white knights to where the black knights are.

Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.

Find an open knight’s tour on a \(2\times2\times2\) cube.

The letters \(A\), \(R\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.
Find \(ART\), given that \(ARTS+STAR=10,T31\).