We solve problems

A pedestrian walked along six streets of one city, passing each street exactly twice, but could not get around them, having passed each one only once. Could this be?

Problem #PRU-103815

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Dissections with certain properties Fun Problems Word Problems Tables and tournaments Tables and tournaments (other)

11–11 2.0

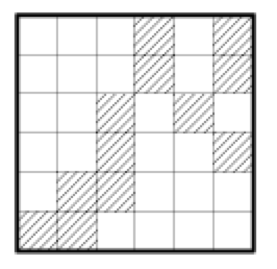
Cut the board shown in the figure into four congruent parts so that each of them contains three shaded cells. Where the shaded cells are placed in each part need not be the same.

Problem #PRU-104045

Problems Fun Problems Word Problems

12–13 2.0

a) In how many ways can Dima paint five Christmas trees in silver, green and blue colours, if the amount of paint is unlimited, and he paints each tree in only one colour?

b) Dima has five baubles: a red, a green, a yellow, a blue and a gold one. In how many ways can he decorate five Christmas trees with them, if he needs to put exactly one bauble on each tree?

c) What about if he can hang several baubles on one Christmas tree (and all of the baubles have to be used)?

Problem #PRU-105052

Problems Methods Pigeonhole principle Pigeonhole principle (other) Proof by contradiction Fun Problems Word Problems Tables and tournaments Tables and tournaments (other)

11–13 3.0

In a chess tournament, each participant played two games with each of the other participants: one with white pieces, the other with black. At the end of the tournament, it turned out that all of the participants scored the same number of points (1 point for a victory, \(\frac{1}{2}\) a point for a draw and 0 points for a loss). Prove that there are two participants who have won the same number of games using white pieces.

Problem #PRU-105208

Problems Fun Problems Word Problems Tables and tournaments Number tables and its properties Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 4.0

A teacher filled the squares of a chequered table with \(5\times5\) different integers and gave one copy of it to Janine and one to Zahara. Janine selects the largest number in the table, then she deletes the row and column containing this number, and then she selects the largest number of the remaining integers, then she deletes the row and column containing this number, etc. Zahara performs similar operations, each time choosing the smallest numbers. Can the teacher fill up the table in such a way that the sum of the five numbers chosen by Zahara is greater than the sum of the five numbers chosen by Janine?

Problem #PRU-107802

Problems Methods Examples and counterexamples. Constructive proofs Fun Problems Word Problems Tables and tournaments Number tables and its properties Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Eight schoolchildren solved \(8\) tasks. It turned out that \(5\) schoolchildren solved each problem. Prove that there are two schoolchildren, who solved every problem at least once.
If each problem is solved by \(4\) pupils, prove that it is not necessary to have two schoolchildren who would solve each problem.

Problem #PRU-107821

Problems Fun Problems Word Problems Tables and tournaments Chessboards and chess pieces Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 3.0

Some squares on a chess board contain a chess piece. It is known that each row contains at least one chess piece, but that different rows all have different numbers of pieces. Prove that it is always possible to mark 8 pieces so that each row and each column of the board contains exactly one marked piece.

Problem #PRU-109476

Problems Fun Problems Word Problems Solving problems by inequalities. Going through the cases. Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

11–14 2.0

Sarah believes that two watermelons are heavier than three melons, Anna believes that three watermelons are heavier than four melons. It is known that one of the girls is right, and the other is mistaken. Is it true that 12 watermelons are heavier than 18 melons? (It is believed that all watermelons weigh the same and all melons weigh the same.)

Problem #PRU-109527

Problems Methods Pigeonhole principle Pigeonhole principle (other) Proof by contradiction Fun Problems Word Problems Tables and tournaments Tables and tournaments (other)

11–13 3.0

What is the largest number of counters that can be put on the cells of a chessboard so that on each horizontal, vertical and diagonal (not only on the main ones) there is an even number of counters?

Problem #PRU-109766

Problems Fun Problems Word Problems Tables and tournaments Number tables and its properties Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Is it possible to arrange natural numbers from 1 to \(2002^2\) in the cells of a \(2002\times2002\) table so that for each cell of this table one could choose a triplet of numbers, from a row or column, where one of the numbers is equal to the product of the other two?