Problems
Several Top Secret Objects are connected by an underground railway in such a way that each Object is directly connected to no more than three others and from each Object one can reach any other Object by going and by changing no more than once. What is the maximum number of Top Secret Objects?
We want to color each of the 15 segments in the picture below using three colors. We need to color them so that if two segments share a point, then they are not the same color. For example, you cannot have both \(AB\) and \(BC\) be blue since they share the end \(B\). Is such a painting possible?
There is a scout group where some of the members know each other. Amongst any four members there is at least one of them who knows the other three. Prove that there is at least one member who knows the entirety of the scout group.
In a distant village, there are \(3\) houses and \(3\) wells. Inhabitants of each house want to have access to all \(3\) wells. Is it possible to build non-intersecting straight paths from each house to each well? All houses and well must be level (that is, none of them are higher up, like on a mountain, nor are any of them on lower ground, like in a valley).
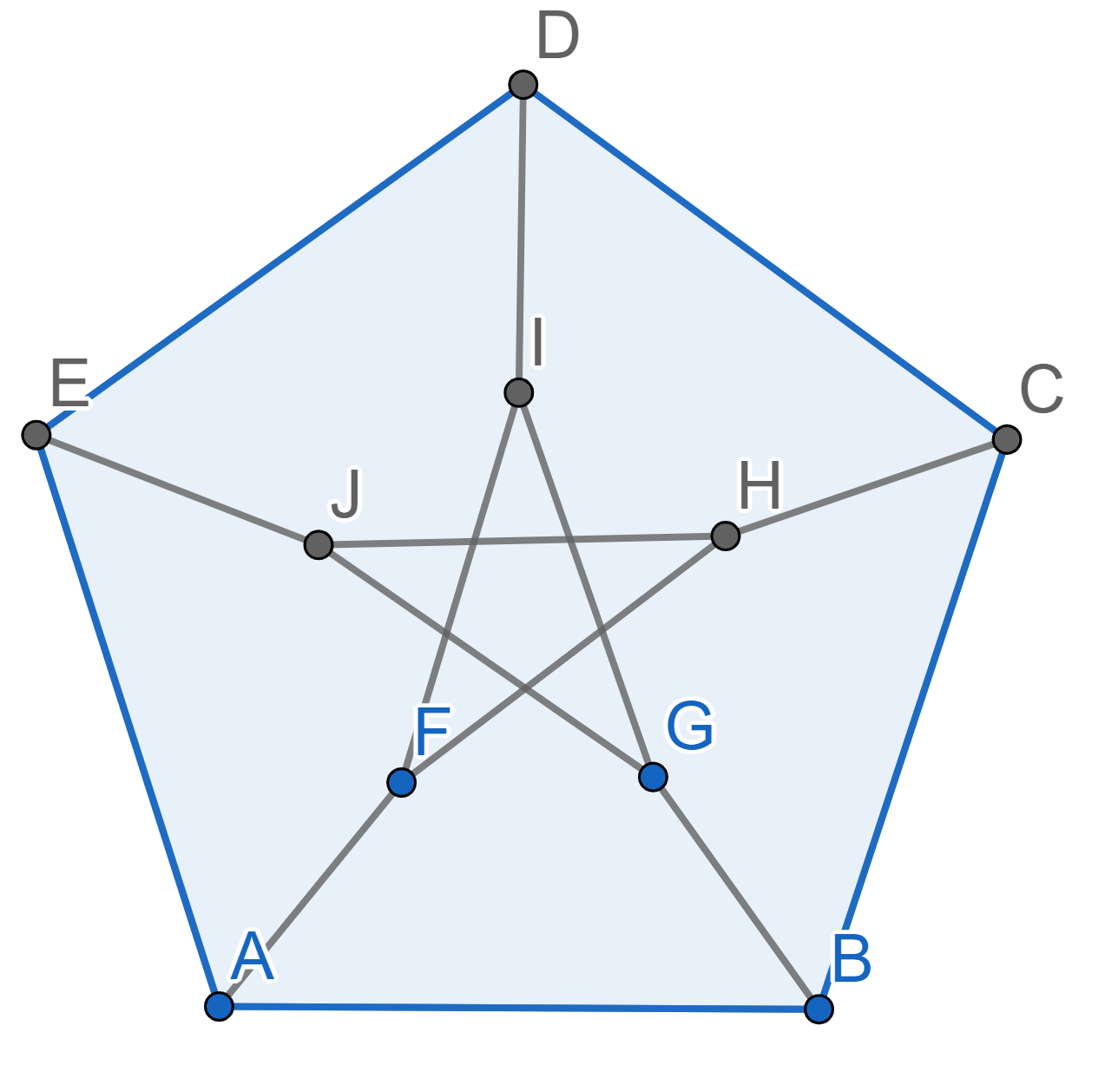
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.
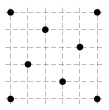
Starting at one of the vertices, an ant wishes to walk each of the \(12\) edges of a sugar cube exactly once. Prove that this is impossible.
Noah has \(10\) dogs, who he wishes
to group into \(5\) pairs for \(5\) families, each of whom want two dogs.
However, the dogs are quite picky, and can’t be paired with most of the
other dogs. None in the first group will go with each other: an
alsatian, a border collie, a chihuahua, a dachshund and an English
bulldog. None in the second group will go with each other: a foxhound, a
greyhound, a harrier, an Irish setter and a Jack Russell.
Furthermore,
The alsatian is the least picky and can be paired with any in the second
group.
The border collie won’t go with the foxhound, but will go with any other dog in the second group.
The chihuahua and the dachshund will only go with the Irish setter and the Jack Russell.
Additionally, none of the foxhound, greyhound and harrier will go
with the English bulldog.
Is it possible to pair up the \(10\)
dogs?