Problems
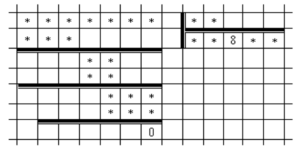
Decipher the following rebus (see the figure). Despite the fact that only two figures are known here, and all others are replaced by asterisks, the example can be restored.
In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.
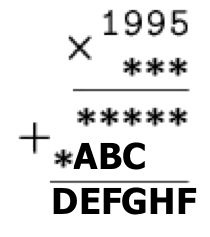
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.
Three people A, B, C counted a bunch of balls of four colors (see table).
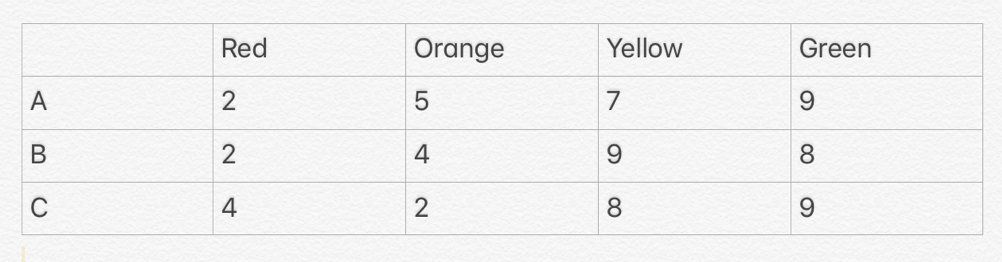
Each of them correctly distinguished some two colors, and confused the numbers of the other two colours: one mixed up the red and orange, another – orange and yellow, and the third – yellow and green. The results of their calculations are given in the table.
How many balls of each colour actually were there?
A family went to the bridge at night. The dad can cross over it in 1 minute, the mom can cross it in 2, the child takes 5 minutes, and grandmother in 10 minutes. They have one flashlight. The bridge can only withstands two people at a time. How can they all cross the bridge in 17 minutes? (If two people pass, then they go at the lower of their speeds.) You can not move along a bridge without a flashlight. You can not shine it from a distance.
On the island of Contrast, both knights and liars live. Knights always tell the truth, liars always lie. Some residents said that the island has an even number of knights, and the rest said that the island has an odd number of liars. Can the number of inhabitants of the island be odd?
Jessica, Nicole and Alex received 6 coins between them: 3 gold coins and 3 silver coins. Each of them received 2 coins. Jessica doesn’t know which coins the others received but only which coins she has. Think of a question which Jessica can answer with either “yes”, “no” or “I don’t know” such that from the answer you can know which coins Jessica has.
There is a rectangular table. Two players start in turn to place on it one pound coin each, so that these coins do not overlap one another. The player who cannot make a move loses. Who will win with the correct strategy?
a) Two players play in the following game: on the table there are 7 two pound coins and 7 one pound coins. In a turn it is allowed to take coins worth no more than three pounds. The one who takes the last coin wins. Who will win with the correct strategy?
b) The same question, if there are 12 one pound and 12 two pound coins.
On Easter Island, people ask each other questions, to which only “yes” or “no” can be answered. In this case, each of them belongs exactly to one of the tribes either A or B. People from tribe A ask only those questions to which the correct answer is “yes”, and from tribe B – those questions to which the correct answer is “no.” In one house lived a couple Ethan and Violet Russell. When Inspector Krugg approached the house, the owner met him on the doorstep with the words: “Tell me, do Violet and I belong to tribe B?”. The inspector thought and gave the right answer. What was the right answer?
There is a \(5\times 9\) rectangle drawn on squared paper. In the lower left corner of the rectangle is a button. Kevin and Sophie take turns moving the button any number of squares either to the right or up. Kevin goes first. The winner is the one who places the button in upper right corner. Who would win, Kevin or Sophie, by using the right strategy?