Problems
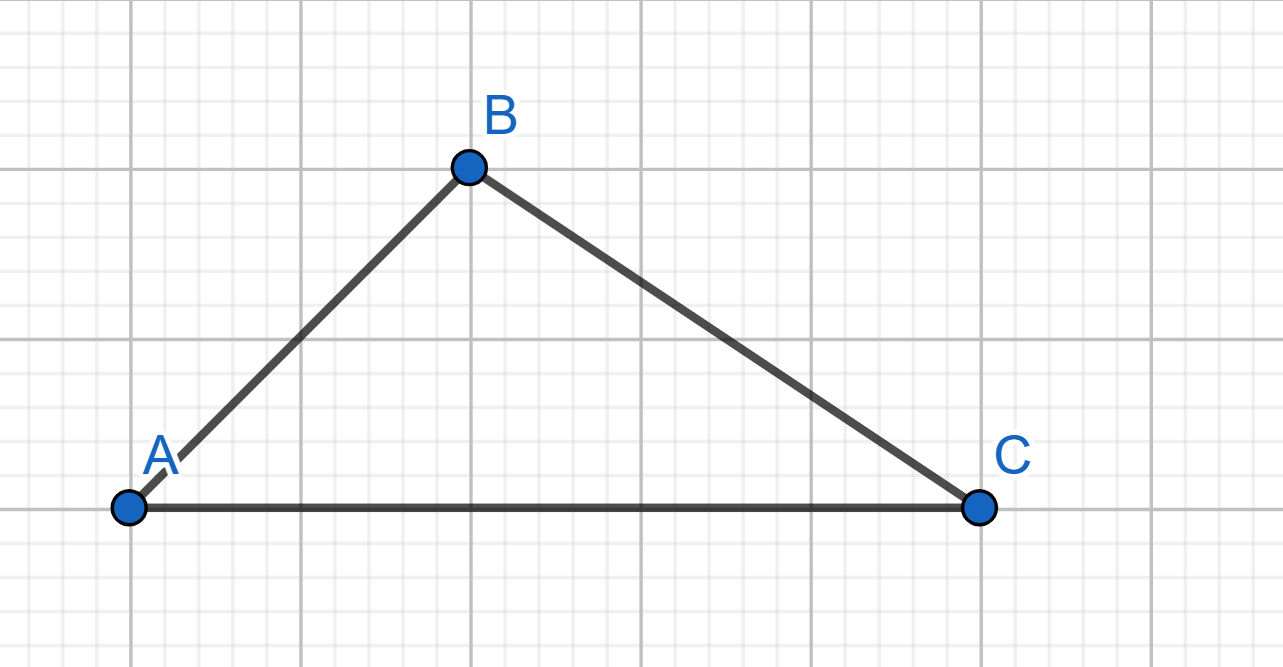
Show how to cover the plane with triangles of the following shape.
Draw how to tile the whole plane with figures, made from squares \(1\times 1\), \(2\times 2\), \(3\times 3\), and \(4\times 4\), where squares are used the same amount of times in the design of the figure.
Show how to cover the plane with convex quadrilaterals.
Draw the plane tiling with:
squares;
rectangles \(1\times 3\);
regular triangles;
regular hexagons.
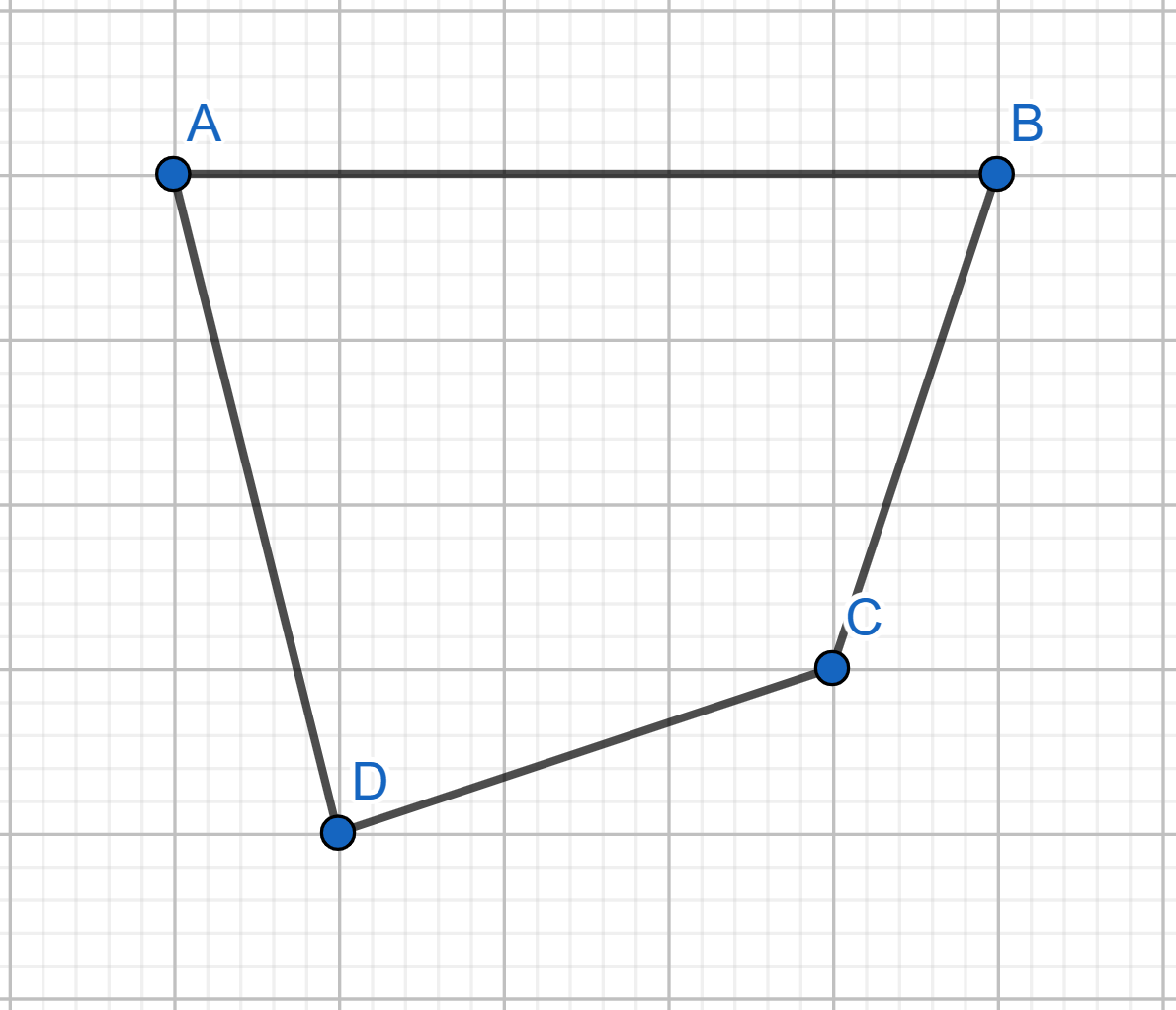
Draw the plane tiling using trapeziums of the following shape:
Here the sides \(AB\) and \(CD\) are parallel.
For any triangle, prove you can tile the plane with that triangle.
Prove that one cannot tile the whole plane with regular pentagons.
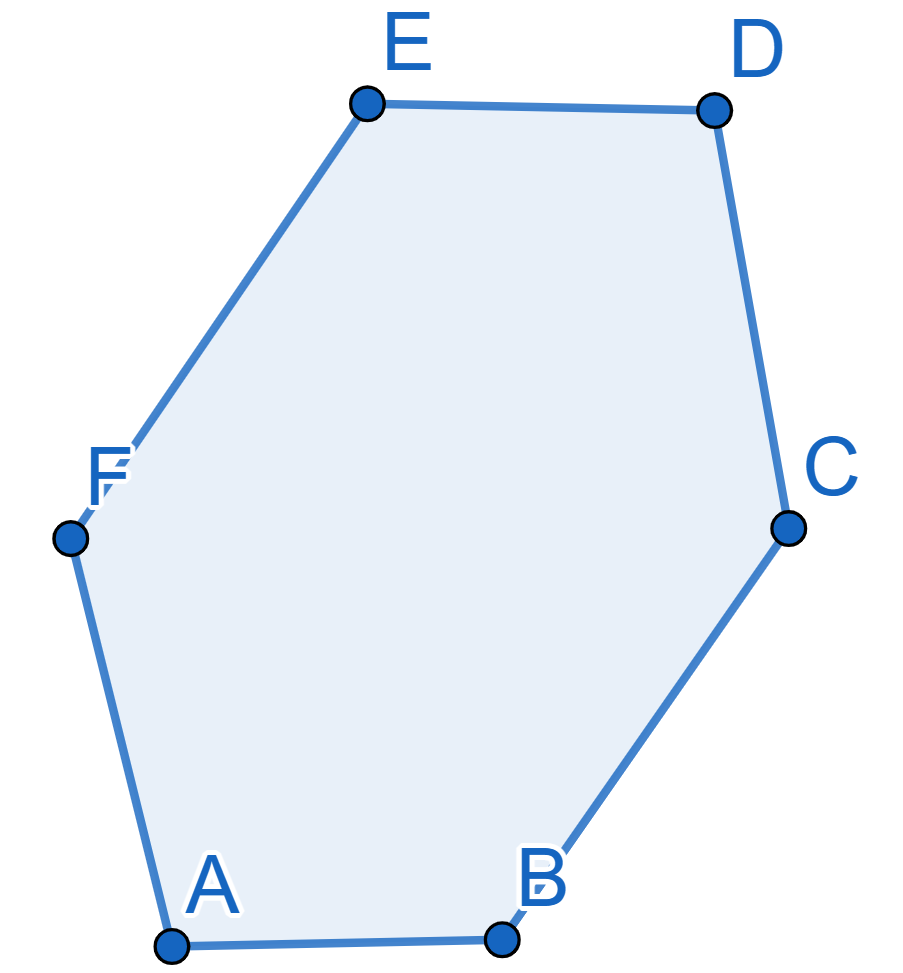
Draw the plane tiling using convex hexagons with parallel and equal opposite sides.
Draw how to tile the whole plane with figures, consisting of squares \(1\times 1\), \(2\times 2\), \(3\times 3\), \(4\times 4\), \(5\times 5\), and \(6\times 6\), where each square appears an equal number of times in the design of the figure. Can you think of two essentially different ways to do this?
Find a non-regular octagon which you can use to tile the whole plane and show how to do that.