Problems

Is it possible to fill a \(5 \times 5\) board with \(1 \times 2\) dominoes?

One corner square was cut from a chessboard. What is the smallest number of equal triangles that can be cut into this shape?

Some open sectors – that is sectors of circles with infinite radii – completely cover a plane. Prove that the sum of the angles of these sectors is no less than \(360^\circ\).

10 magazines lie on a coffee table, completely covering it. Prove that you can remove five of them so that the remaining magazines will cover at least half of the table.

A straight corridor of length 100 m is covered with 20 rugs that have a total length of 1 km. The width of each rug is equal to the width of the corridor. What is the longest possible total length of corridor that is not covered by a rug?

Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(6\times 6\) rectangle?

Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(6\times8\) rectangle.

In the picture below, there are the \(12\) pentominoes. Is it possible to tile a \(6\times10\) rectangle with them, using each pentominoe exactly once?

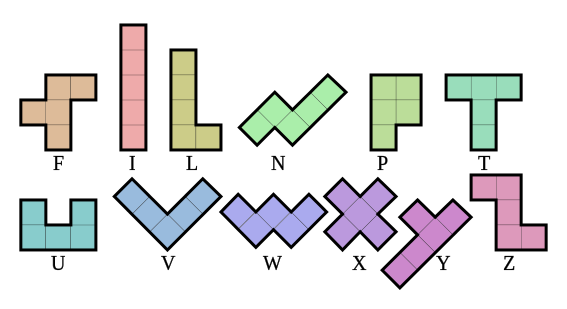
Show how to tile a \(5\times12\) rectangle with the twelve pentominoes.

Show how to tile a \(4\times15\) rectangle with the twelve pentominoes.