Problems
Suppose that \((x_1,y_1),(x_2,y_2)\) are solutions to Pell’s equation \(x^2-dy^2 = 1\). Show that \((x_1x_2+dy_1y_2,x_1y_2+x_2y_2)\) also satisfies the same equation.
Suppose that \(x+y\sqrt{d}>1\) gives a solution to Pell’s equation. Show that \(x\geq 2\) and \(y\geq 1\). Can the bounds be achieved?
Every year the citizens of the planet “Lotsofteeth" enter a contest
to see who has the most teeth.
This year the judge notices:
Nobody has 0 teeth (everyone has at least 1).
There are more people in the contest than the most teeth that any one person has. (For example, if the most teeth anyone has is 27, then there are more than 27 people participating in the contest.)
Must there be two people who have exactly the same number of teeth? Explain why.
Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?
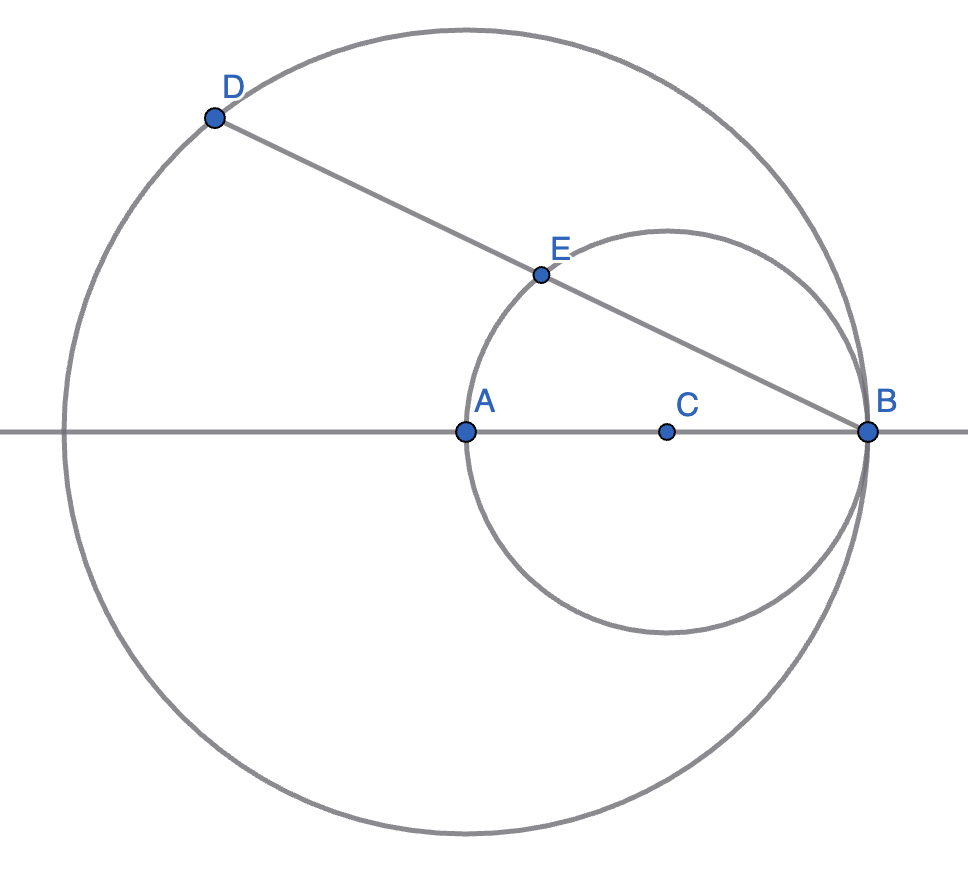
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
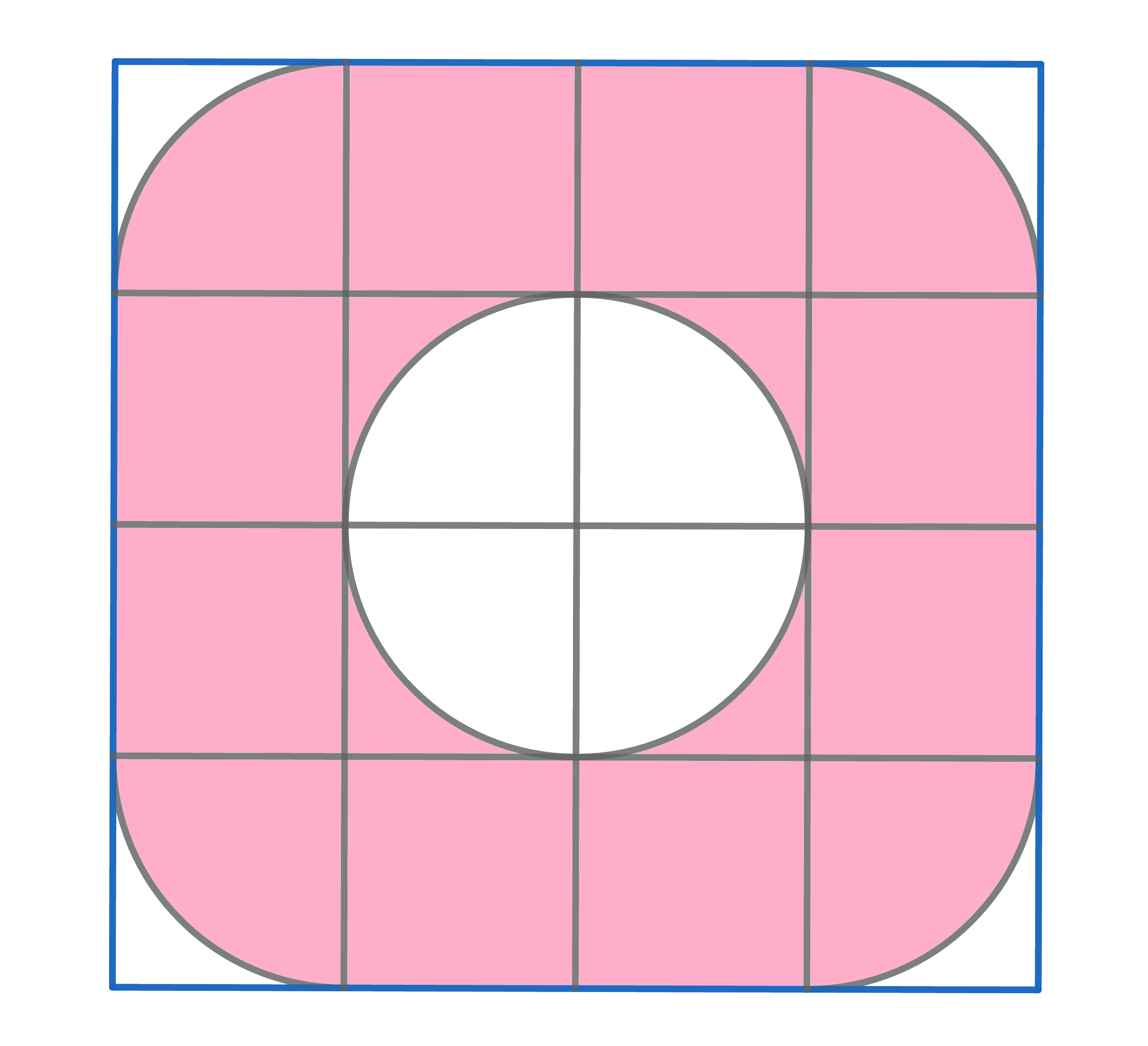
The area of the coloured figure equals \(48\)cm\(^2\). Find the length of the side of the smallest square.
The director of a bank has forgotten the combination to open the safe! He only remembers the first \(8\) out of \(10\) digits, and that the whole number was divisible by \(45\). Help him out and find all possible pairs of digits which could complete the combination. \[20242025**\]
There are two hourglasses, a small one and a large one. The sand in the small one takes \(7\) minutes to fall all the way through, and the sand in the large one takes \(11\) minutes. How can you measure \(15\) minutes using those?
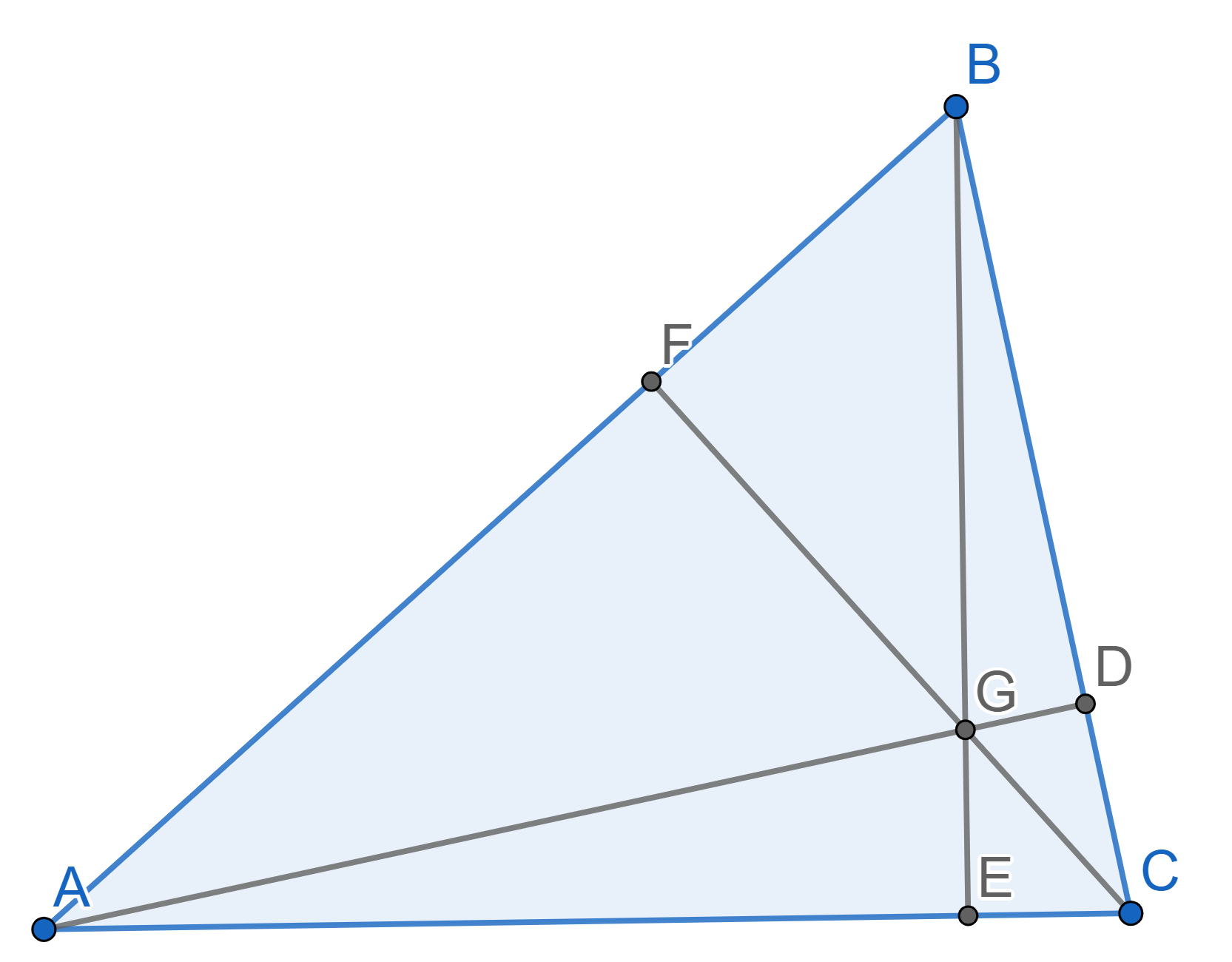
Let \(ABC\) be a non-isosceles
triangle. The point \(G\) is the point
of intersection of the medians \(AE\),
\(BF\), \(CD\). The point \(H\) is the point of intersection of all
heights. The point \(I\) is the center
of the circumscribed circle of \(ABC\),
or the point of intersection of all perpendicular bisectors to the
segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one
line and that the ratio \(IG:GH =
1:2\). The line that all of \(I\), \(G\)
and \(H\) lie on is called the
Euler line of triangle \(ABC\).
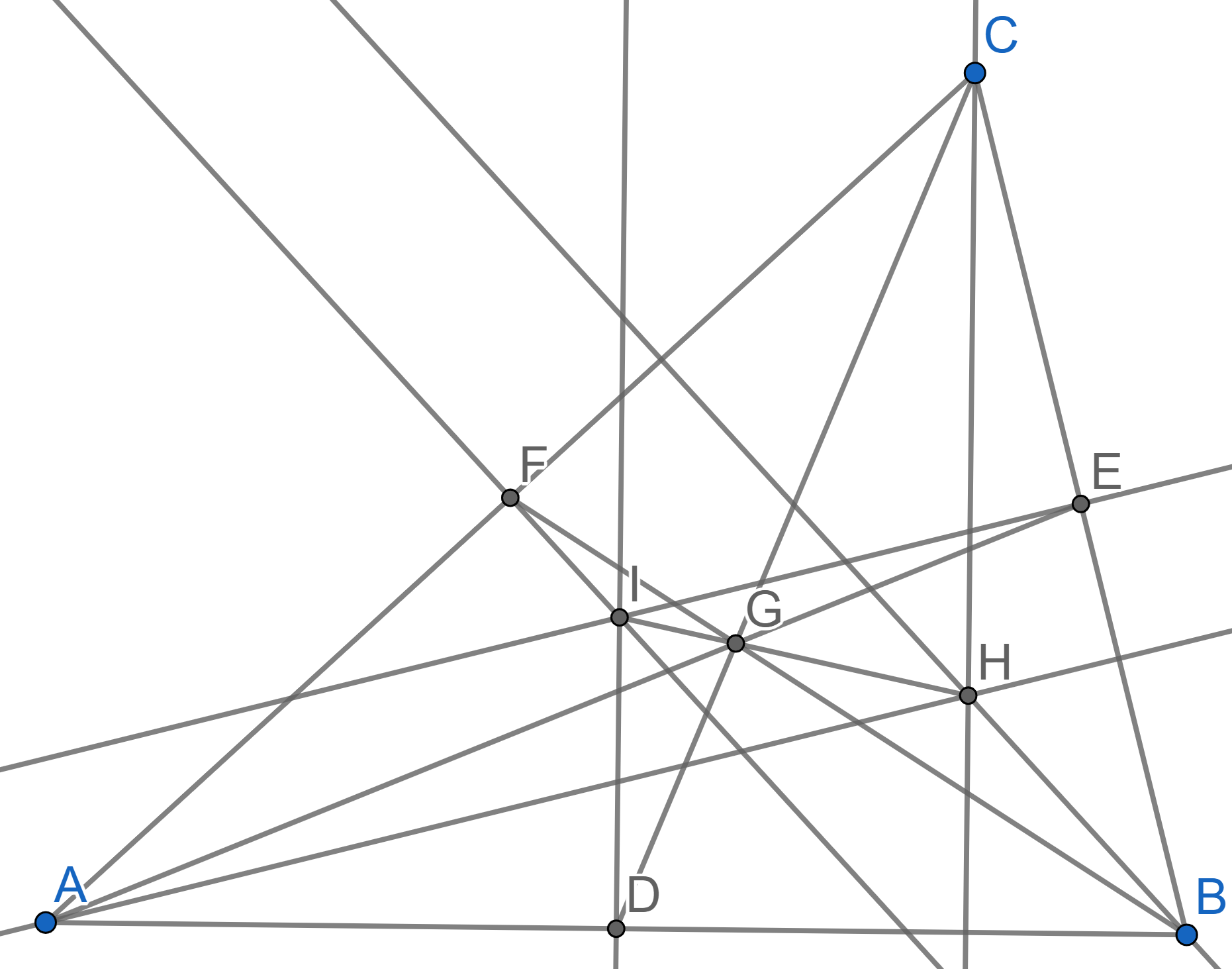
Let \(ABC\) be a triangle. Prove that the heights \(AD\), \(BE\), \(CF\) intersect in one point.