We solve problems

Problem #PRU-110166

Problems Discrete Mathematics Algorithm Theory Balance puzzles Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

A set of weights has the following properties: It contains \(5\) weights, which are all different in weight. For any two weights, there are two other weights of the same total weight. What is the smallest number of weights that can be in this set?

Problem #PRU-110185

Problems Methods Pigeonhole principle Pigeonhole principle (other) Fun Problems Word Problems Tables and tournaments Tournament tables

12–14 3.0

Five teams participated in a football tournament. Each team had to play exactly one match with each of the other teams. Due to financial difficulties, the organisers cancelled some of the games. As a result, it turned out that all teams scored a different number of points and no team scored zero points. What is the smallest number of games that could be played in the tournament, if three points were awarded for a victory, one for a draw and zero for a defeat?

Problem #PRU-111000

Problems Discrete Mathematics Combinatorics Integer lattices Integer lattices (other) Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 3.0

Inside a square with side 1 there are several circles, the sum of the radii of which is 0.51. Prove that there is a line that is parallel to one side of the square and that intersects at least 2 circles.

Problem #PRU-111328

Problems Fun Problems Word Problems Tables and tournaments Number tables and its properties Methods Pigeonhole principle Pigeonhole principle (other)

12–14 3.0

A cinema contains 7 rows each with 10 seats. A group of 50 children went to see the morning screening of a film, and returned for the evening screening. Prove that there will be two children who sat in the same row for both the morning and the evening screening.

Problem #PRU-111682

Problems Fun Problems Word Problems Tables and tournaments Chessboards and chess pieces Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Proof by contradiction

12–14 3.0

100 queens, that cannot capture each other, are placed on a \(100 \times 100\) chessboard. Prove that at least one queen is in each \(50 \times 50\) corner square.

Problem #PRU-115384

Problems Discrete Mathematics Combinatorics Geometry on grid paper Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 4.0

A game of ’Battleships’ has a fleet consisting of one \(1\times 4\) square, two \(1\times 3\) squares, three \(1\times 2\) squares, and four \(1\times 1\) squares. It is easy to distribute the fleet of ships on a \(10\times 10\) board, see the example below. What is the smallest square board on which this fleet can be placed? Note that by the rules of the game, no two ships can be placed on horizontally, vertically, or diagonally adjacent squares.

Problem #PRU-115449

Problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

13–16 4.0

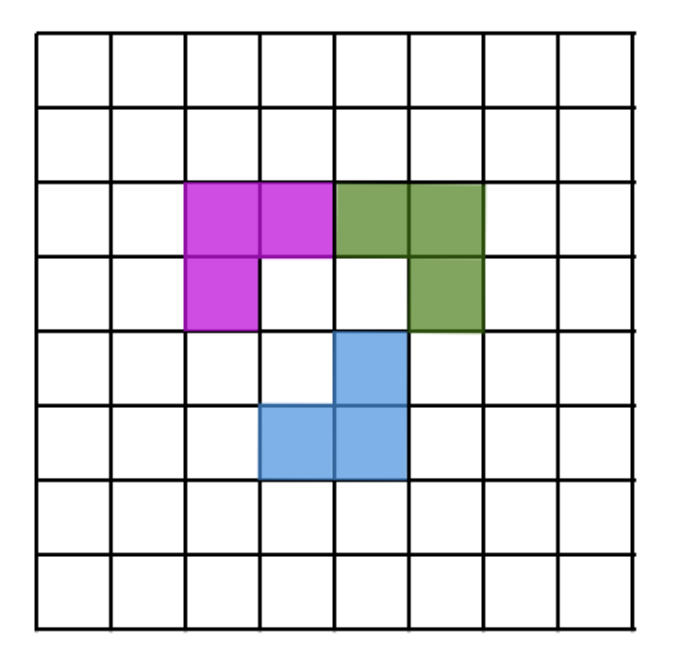
On an 8×8 grid (like a chessboard), an L-corner is a shape made of 3 little squares of the board that touch to make an L. You can turn the L any way you like. We place the L-corners so that none overlap. What is the fewest L-corners you must place so that no more L-corners can be added anywhere? Here is an example of how three L-corners may look like:

Problem #PRU-115489

Problems Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other) Methods Algebraic methods Proof by exhaustion

10–12 2.0

One day, Claudia, Sofia and Freia noticed that they brought the same toy cars to kindergarten. Claudia has a car with a trailer, a small car and a green car without a trailer. Sofia has a car without a trailer and a small green one with a trailer, and Freia has a big car and a small blue car with a trailer. What kind of car (in terms of colour, size and availability of a trailer) did all of the girls bring to the kindergarten? Explain the answer.

Problem #PRU-115492

Problems Methods Algebraic methods Proof by exhaustion Discrete Mathematics Set theory and logic Mathematical logic Puzzles

11–13 2.0

The \(KUB\) is a cube. Prove that the ball, \(CIR\), is not a cube. (\(KUB\) and \(CIR\) are three-digit numbers, where different letters denote different numbers).

Problem #PRU-116435

Problems Fun Problems Word Problems Tables and tournaments Chessboards and chess pieces Methods Pigeonhole principle Pigeonhole principle (other) Proof by contradiction

14–16 3.0

On a chessboard, \(n\) white and \(n\) black rooks are arranged so that the rooks of different colours cannot capture one another. Find the greatest possible value of \(n\).