Problems

A page of a calendar is partially covered by the previous torn sheet (see the figure). The vertices A and B of the upper sheet lie on the sides of the bottom sheet. The fourth vertex of the lower leaf is not visible – it is covered by the top sheet. The upper and lower pages, of course, are identical in size to each other. Which part of the lower page is greater, that which is covered or that which is not?

The population of China is one billion people. It would seem that on a map of China with a scale of 1 : 1,000,000 (1 cm : 10 km), it would be possible to fit a million times fewer people than there is in the whole country. However, in fact, not only 1000, but even 100 people will not be able to be placed on this map. Can you explain this contradiction?

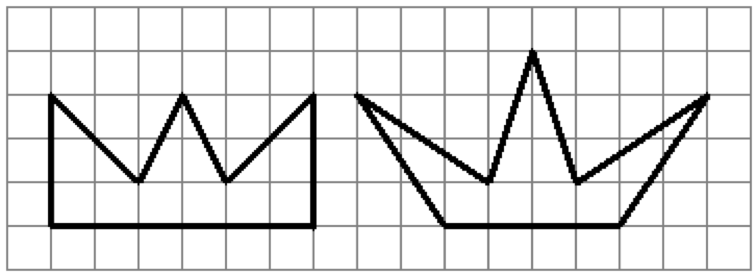
Find the area of the figures shown below.

101 random points are chosen inside a unit square, including on the edges of the square, so that no three points lie on the same straight line. Prove that there exist some triangles with vertices on these points, whose area does not exceed 0.01.

9 straight lines each divide a square into two quadrilaterals, with their areas having a ratio of \(2:3\). Prove that at least three of the nine lines pass through the same point.

Let \(E\) and \(F\) be the midpoints of the sides \(BC\) and \(AD\) of the parallelogram \(ABCD\). Find the area of the quadrilateral formed by the lines \(AE, ED, BF\) and \(FC\), if it is known that the area \(ABCD\) is equal to \(S\).

A polygon is drawn around a circle of radius \(r\). Prove that its area is equal to \(pr\), where \(p\) is the semiperimeter of the polygon.

The point \(E\) is located inside the parallelogram \(ABCD\). Prove that \(S_{ABE} + S_{CDE} = S_{BCE} + S_{ADE}\).

The diagonals of the quadrilateral \(ABCD\) intersect at the point \(O\). Prove that \(S_{AOB} = S_{COD}\) if and only if \(BC \parallel AD\).

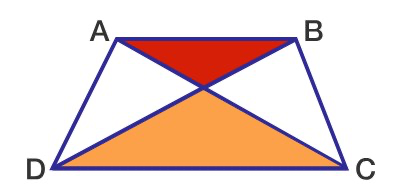
The area of the red triangle is \(25\) and the area of the orange triangle is \(49\). What is the area of the trapezium \(ABCD\)?