Problems

Inside a square with side 1 there are several circles, the sum of the radii of which is 0.51. Prove that there is a line that is parallel to one side of the square and that intersects at least 2 circles.

100 queens, that cannot capture each other, are placed on a \(100 \times 100\) chessboard. Prove that at least one queen is in each \(50 \times 50\) corner square.

A game of ’Battleships’ has a fleet consisting of one \(1\times 4\) square, two \(1\times 3\) squares, three \(1\times 2\) squares, and four \(1\times 1\) squares. It is easy to distribute the fleet of ships on a \(10\times 10\) board, see the example below. What is the smallest square board on which this fleet can be placed? Note that by the rules of the game, no two ships can be placed on horizontally, vertically, or diagonally adjacent squares.

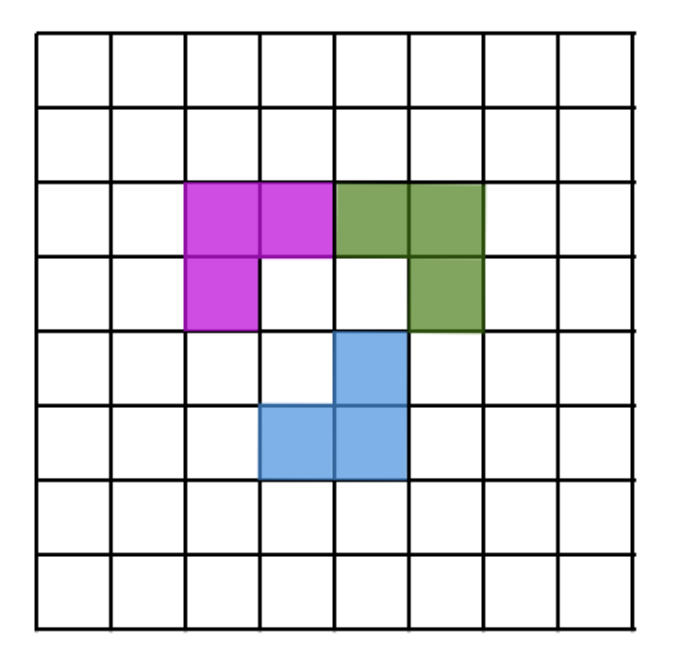
On an 8×8 grid (like a chessboard), an L-corner is a shape made of 3 little squares of the board that touch to make an L. You can turn the L any way you like. We place the L-corners so that none overlap. What is the fewest L-corners you must place so that no more L-corners can be added anywhere? Here is an example of how three L-corners may look like:

10 children, including Billy, attended Billy’s birthday party. It turns out that any two children picked from those at the party share a grandfather. Prove that 7 of the children share a grandfather.

101 random points are chosen inside a unit square, including on the edges of the square, so that no three points lie on the same straight line. Prove that there exist some triangles with vertices on these points, whose area does not exceed 0.01.

A scone contains raisins and sultanas. Prove that inside the scone there will always be two points 1cm apart such that either both lie inside raisins, both inside sultanas, or both lie outside of either raisins or sultanas.

101 points are marked on a plane; not all of the points lie on the same straight line. A red pencil is used to draw a straight line passing through each possible pair of points. Prove that there will always be a marked point on the plane through which at least 11 red lines pass.

9 straight lines each divide a square into two quadrilaterals, with their areas having a ratio of \(2:3\). Prove that at least three of the nine lines pass through the same point.

A Cartesian plane is coloured in in two colours. Prove that there will be two points on the plane that are a distance of 1 apart and are the same colour.