Problems
A game of ’Battleships’ has a fleet consisting of one \(1\times 4\) square, two \(1\times 3\) squares, three \(1\times 2\) squares, and four \(1\times 1\) squares. It is easy to
distribute the fleet of ships on a \(10\times
10\) board, see the example below. What is the smallest square
board on which this fleet can be placed? Note that by the rules of the
game, no two ships can be placed on horizontally, vertically, or
diagonally adjacent squares.

One corner square was cut from a chessboard. What is the smallest number of equal triangles that can be cut into this shape?
The city plan is a rectangle of \(5 \times 10\) cells. On the streets, a one-way traffic system is introduced: it is allowed to go only to the right and upwards. How many different routes lead from the bottom left corner to the upper right?
On a \(100 \times 100\) board 100 rooks are placed that cannot capturing one another.
Prove that an equal number of rooks is placed in the upper right and lower left cells of \(50 \times 50\) squares.
On the grid paper, Theresa drew a rectangle \(199 \times 991\) with all sides on the grid lines and vertices on intersection of grid lines. How many cells of the grid paper are crossed by a diagonal of this rectangle?
In the \(6\times7\) large rectangle shown below, how many rectangles are there in total formed by grid lines?

Imagine a \(5\times6\) rectangular chocolate bar, and you want to split it between you and your \(29\) closest friends, so that each person gets one square. You repeatedly snap the chocolate bar along the grid lines until the rectangle is in \(30\) individual squares. You can’t snap more than one rectangle at a time.


The diagram shows a couple of choices for your first two snaps. For
example, in the first picture, you snap along a vertical line, and then
snap the left rectangle along a horizontal line.
How many snaps do you need to get the \(30\) squares?
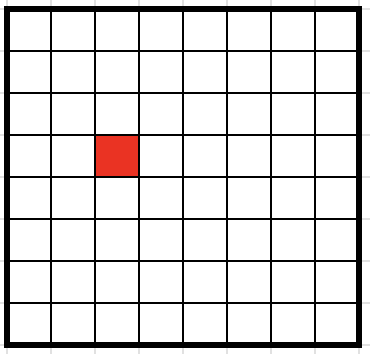
Prove that it’s impossible to cover a \(4\times9\) rectangle with \(9\) ‘T’ tetrominoes (one copy seen in red).


One square is coloured red at random on an \(8\times8\) grid. Show that no matter where this red square is, you can cover the remaining \(63\) squares with \(21\) ‘L’ triominoes, with no gaps or overlaps.