Problems

With a non-zero number, the following operations are allowed: \(x \rightarrow \frac{1+x}{x}\), \(x \rightarrow \frac{1-x}{x}\). Is it true that from every non-zero rational number one can obtain each rational number with the help of a finite number of such operations?

Seven triangular pyramids stand on the table. For any three of them, there is a horizontal plane that intersects them along triangles of equal area. Prove that there is a plane intersecting all seven pyramids along triangles of equal area.

Prove that for all \(x\), \(0 < x < \pi /3\), we have the inequality \(\sin 2x + \cos x > 1\).

Is there a sequence of natural numbers in which every natural number occurs exactly once, and for any \(k = 1, 2, 3, \dots\) the sum of the first \(k\) terms of the sequence is divisible by \(k\)?

At all rational points of the real line, integers are arranged. Prove that there is a segment such that the sum of the numbers at its ends does not exceed twice the number on its middle.

Prove that for any positive integer \(n\) the inequality

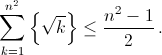
is true.

Ten pairwise distinct non-zero numbers are such that for each two of them either the sum of these numbers or their product is a rational number.

Prove that the squares of all numbers are rational.

The polynomial \(P (x)\) of degree \(n\) has \(n\) distinct real roots.

What is the largest number of its coefficients that can be equal to zero?

For which \(\alpha\) does there exist a function \(f\colon \mathbb{R} \rightarrow \mathbb{R}\) that is not a constant, such that \(f (\alpha (x + y)) = f (x) + f (y)\)?

The sum of the positive numbers \(a, b, c\) is \(\pi / 2\). Prove that \(\cos a + \cos b + \cos c > \sin a + \sin b + \sin c\).