Problems
40% of adherents of some political party are women. 70% of the adherents of this party are townspeople. At the same time, 60% of the townspeople who support the party are men. Are the events “the adherent of the party is a townsperson” and “the adherent of party is a woman” independent?
The tower in the castle of King Arthur is crowned with a roof, which is a triangular pyramid, in which all flat angles at the top are straight. Three roof slopes are painted in different colours. The red roof slope is inclined to the horizontal at an angle \(\alpha\), and the blue one at an angle \(\beta\). Find the probability that a raindrop that fell vertically on the roof in a random place fell on the green area.
a) There is an unlimited set of cards with the words “abc”, “bca”, “cab” written. Of these, the word written is determined according to this rule. For the initial word, any card can be selected, and then on each turn to the existing word, you can either add on a card to the left or to the right, or cut the word anywhere (between the letters) and put a card there. Is it possible to make a palindrome with this method?
b) There is an unlimited set of red cards with the words “abc”, “bca”, “cab” and blue cards with the words “cba”, “acb”, “bac”. Using them, according to the same rules, a palindrome was made. Is it true that the same number of red and blue cards were used?
In the triangle \(ABC\), the angle \(A\) is equal to \(40^{\circ}\). The triangle is randomly thrown onto a table. Find the probability that the vertex \(A\) lies east of the other two vertices.
At a factory known to us, we cut out metal disks with a diameter of 1 m. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, a measurement error occurs, and therefore the standard deviation of the radius is 10 mm. Engineer Gavin believes that a stack of 100 disks on average will weigh 10,000 kg. By how much is the engineer Gavin wrong?
Investigating one case, the investigator John Smith discovered that the key witness is the one from the Richardson family who, on that fateful day, came home before the others. The investigation revealed the following facts.
1. The neighbour Maria Ramsden, wanting to borrow some salt from the Richardson’s, rang their doorbell, but no one opened the door. At what time though? Who knows? It was already dark...
2. Jill Richardson came home in the evening and found both children in the kitchen, and her husband was on the sofa – he had a headache.
3. The husband, Anthony Richardson, declared that, when he came home, immediately sat down on the sofa and had a nap. He did not see anyone, nor did he hear anything, and the neighbour definitely did not come – the doorbell would have woken him up.
4. The daughter, Sophie, said that when she returned home, she immediately went to her room, and she does not know anything about her father, however, in the hallway, as always, she stumbled on Dan’s shoes.
5. Dan does not remember when he came home. He also did not see his father, but he did hear how Sophie got angry about his shoes.
“Aha,” thought John Smith. “What is the likelihood that Dan returned home before his father?”.
On weekdays, the Scattered Scientist goes to work along the circle line on the London Underground from Cannon Street station to Edgware Road station, and in the evening he goes back (see the diagram).
Entering the station, the Scientist sits down on the first train that arrives. It is known that in both directions the trains run at approximately equal intervals, and along the northern route (via Farringdon) the train goes from Cannon Street to Edgware Road or back in 17 minutes, and along the southern route (via St James Park) – 11 minutes. According to an old habit, the scientist always calculates everything. Once he calculated that, from many years of observation:
– the train going counter-clockwise, comes to Edgware Road on average 1 minute 15 seconds after the train going clockwise arrives. The same is true for Cannon Street.
– on a trip from home to work the Scientist spends an average of 1 minute less time than a trip home from work.
Find the mathematical expectation of the interval between trains going in one direction.
On one island, one tribe has a custom – during the ritual dance, the leader throws up three thin straight rods of the same length, connected in the likeness of the letter capital \(\pi\), \(\Pi\). The adjacent rods are connected by a short thread and therefore freely rotate relative to each other. The bars fall on the sand, forming a random figure. If it turns out that there is self-intersection (the first and third bars cross), then the tribe in the coming year are waiting for crop failures and all sorts of trouble. If there is no self-intersection, then the year will be successful – satisfactory and happy. Find the probability that in 2019, the rods will predict luck.
Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.
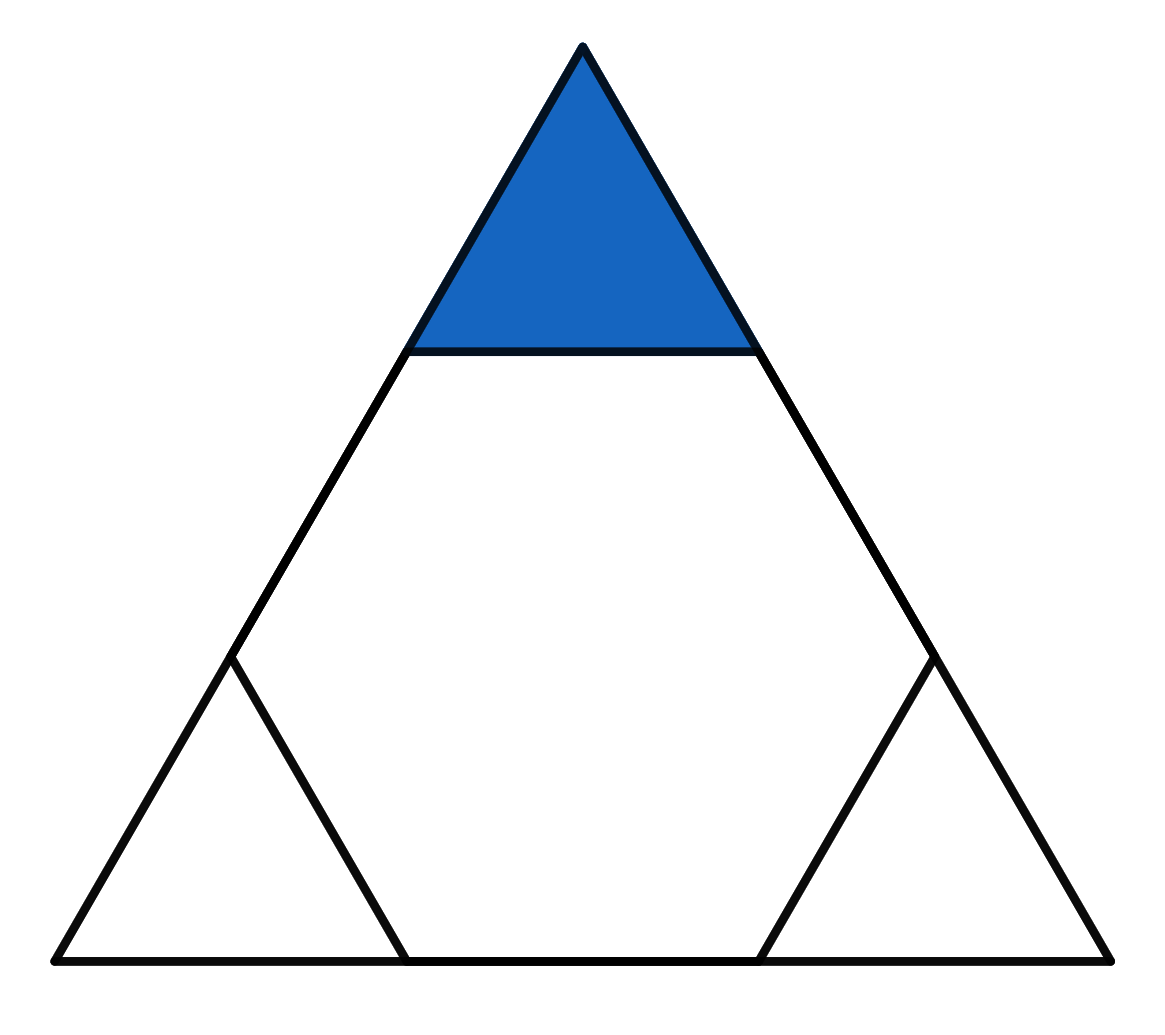
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.