Problems

Multiplication of numbers. Restore the following example of the multiplication of natural numbers if it is known that the sum of the digits of both factors is the same.

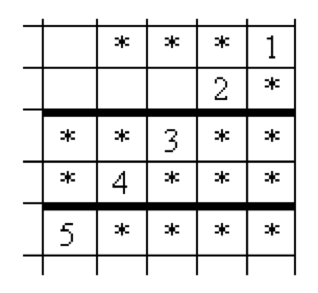
Restore the example of the multiplication.

Prove that the number of all arrangements of the largest possible amount of peaceful bishops (figures that move on diagonals and don’t threaten each other) on the \(8\times 8\) chessboard is an exact square.

There is a 12 litre barrel filled with water, and two empty barrels (one is 5 litres in volume and the other is 8 litres). Using these barrels, try to

a) divide the water into 2 parts with volumes: 3 litres and 9 litres;

b) divide the water into 2 parts with equal volume.

Can there exist two functions \(f\) and \(g\) that take only integer values such that for any integer \(x\) the following relations hold:

a) \(f (f (x)) = x\), \(g (g (x)) = x\), \(f (g (x)) > x\), \(g (f (x)) > x\)?

b) \(f (f (x)) < x\), \(g (g (x)) < x\), \(f (g (x)) > x\), \(g (f (x)) > x\)?

Michael thinks of a number no less than \(1\) and no greater than \(1000\). Victoria is only allowed to ask questions to which Michael can answer “yes” or “no” (Michael always tells the truth). Can Victoria figure out which number Michael thought of by asking \(10\) questions?

There are 6 locked suitcases and 6 keys to them. At the same time, it is not known to which suitcase each key fits. What is the smallest number of attempts you need to make in order to open all the suitcases for sure? And how many attempts will it take there are not 6 but 10 keys and suitcases?

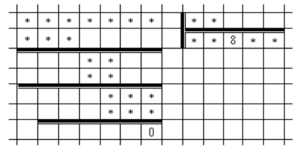
Decipher the following rebus (see the figure). Despite the fact that only two figures are known here, and all others are replaced by asterisks, the example can be restored.

The parliament of a certain country has two houses with an equal number of members. In order to make a decision on an important issue all the members voted and there were no abstentions. When the chairman announced that the decision had been taken with a 23-vote advantage, the opposition leader declared that the results had been rigged. How did he know it?

A resident of one foreign intelligence agency informed the centre about the forthcoming signing of a number of bilateral agreements between the fifteen former republics of the USSR. According to his report, each of them will conclude an agreement exactly with three others. Should this resident be trusted?